液体窒素のキャビテーション流動不安定
極低温液体は宇宙機器の燃料、超伝導機器の冷媒として期待されていますが、キャビテーション現象は詳細に研究されていない。キャビテーション発生時の流動構造の違い、流体振動、熱力学的効果について研究を行なっている。収縮-拡大ノズルにおいて、気液二相化および低温化(サブクール度が大きい)による音速低下が原因で発生するキャビテーションモードの変化(連続から間欠的発生)、流体振動について研究を行なっている
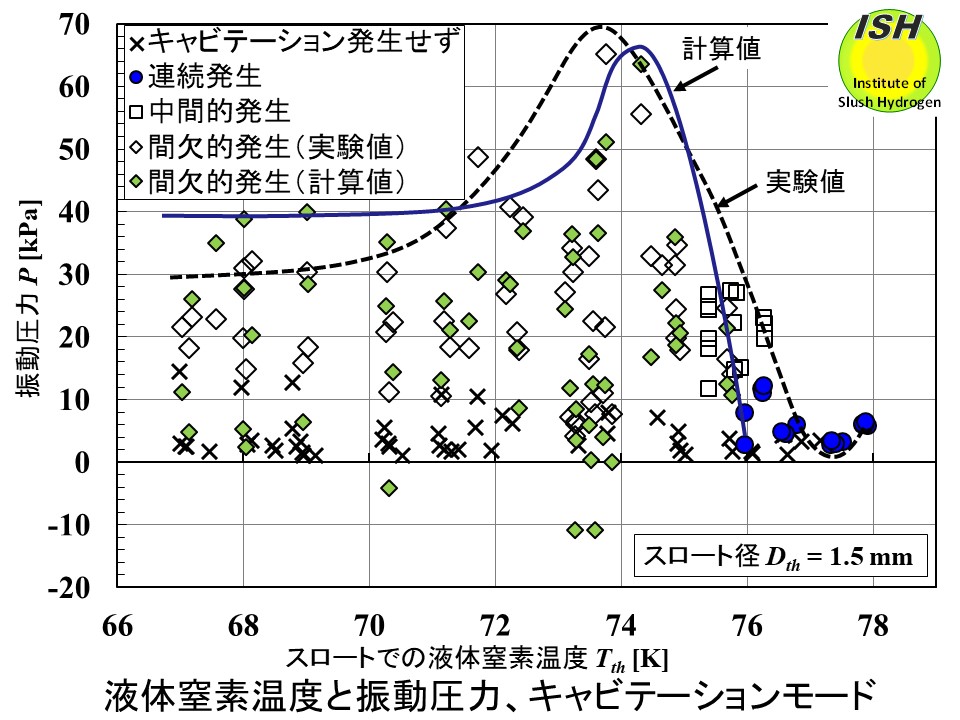
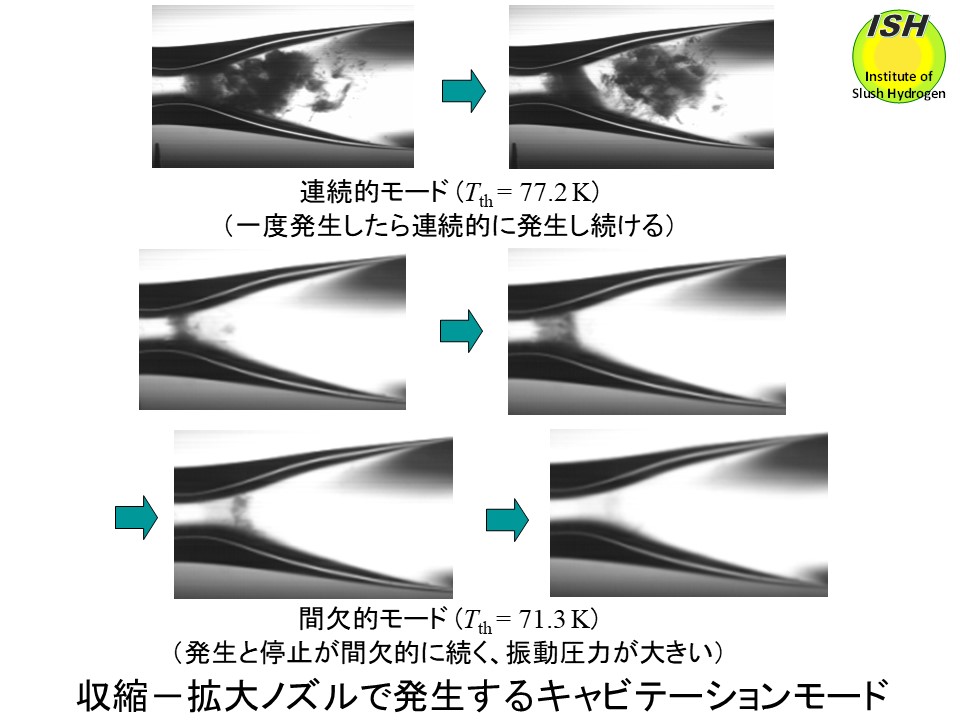
[32, 33]。音速低下に起因する流動不安定の可視化観察結果を上図に、発生する振動圧力を下図に示す。
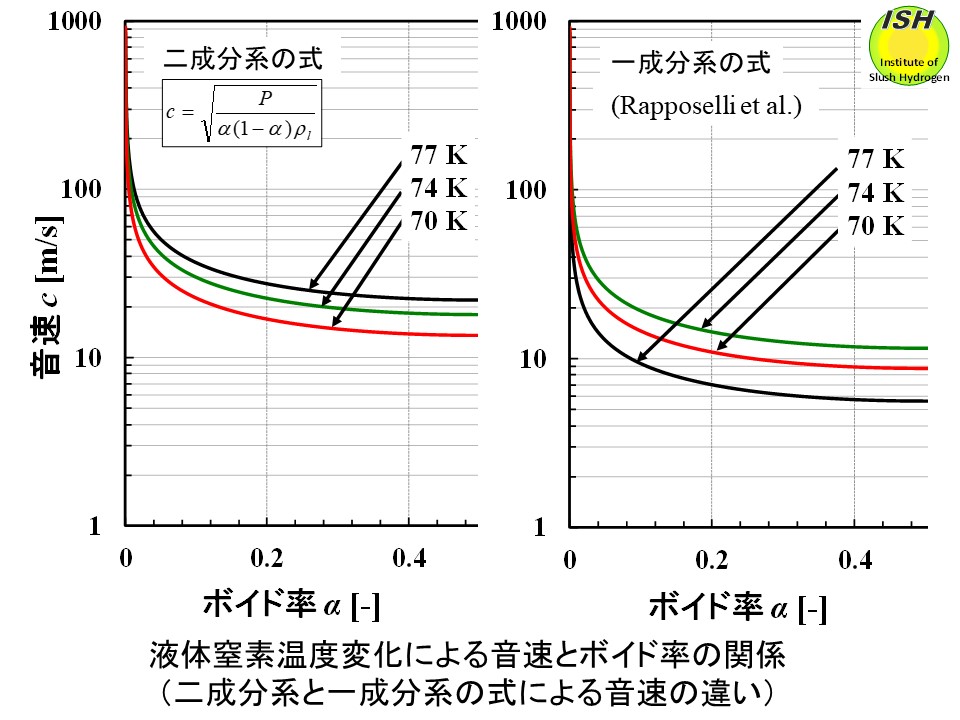
気液二相流体の音速は、液体単相の音速に比べて小さいことは古くから良く知られている。下図に空気-水などの二成分系気液二相流体で使用されている音速の式とボイド率の関係(気体窒素-液体窒素系で計算)、および液体とその蒸気が混在する一成分系気液二相流体(気体窒素-液体窒素系)の音速の式とボイド率の関係 [35]を示す。キャビテーションモードの変化は、液体窒素がキャビテーション発生によって気液二相状態に変化することによる急激な音速低下が原因と考えられる。下図に示すように音速はボイド率がわずかに増加した場合でも液体単相状態と比べて大きく低下する。キャビテーション発生直前の流速と比べて、キャビテーション発生後の気液二相流体の音速が低くなると、スロート部での流速が音速に制限されるチョーク状態となり、流速が急激に低下する。流速が低下すると、スロート静圧が飽和蒸気圧より上昇してキャビテーションは安定した発生を続けることができず、液体単相の流動に戻る。
二成分系の気液二相流体の音速の式を適用した場合について、スロート温度におけるスロート流速とキャビテーションモードの関係を下図に示す。スロート径は 1.5 mmである。スロート流速が音速に制限されることを考慮すると、このキャビテーション初生流速と音速曲線が交差する点から、キャビテーション発生時のスロートでの最大ボイド率を概略見積もることができる。例えば、73 K で0.5、71 K で0.2、68 K で0.1程度と見積もることができ、温度が低くなるほどキャビテーション発生時の最大ボイド率が小さくなる。然しながら、高速度カメラの可視化結果からは、図に示した曲線よりも低いボイド率で音速と流速は干渉していることが観察されている。また、図に示すように、74 K以上の温度領域での音速と流速の干渉が充分説明できない。
次に、一成分系の気液二相流体の音速の式を適用した場合について、下図にスロート温度におけるスロート流速とキャビテーションモードの関係、音速曲線を示す。音速曲線はボイド率 0.03、0.06、0.09、0.12 の場合を表している。二成分系と異なり、各音速曲線(ボイド率一定)において温度75 K 付近で音速が最大となる。間欠的キャビテーションが観察された74 K 以下の温度領域での最大ボイド率は、74 K で 0.12、72 K で 0.09、70 Kで 0.06程度と見積もることができ、温度の低下に伴ってボイド率も小さくなることがわかる。この傾向は、温度の低下に伴ってキャビテーションが発生し難くなり、たとえ発生したとしても温度の高い条件に比べ、スロートでのボイド率が小さいという可視化観測結果と良く一致している。従って、一成分系気液二相流体の音速がキャビテーション発生時にスロート流速を制限するチョーク現象が発生しており、これによってキャビテーションモードが変化していることが初めて実証された。
キャビテーション発生時の振動圧力の大きさは、温度74~76 Kで最大値となった。即ち、キャビテーションが発生する中間的発生および間欠的発生において、スロート径1.5
mm の場合は 76 K 付近で30 kPa,スロート径2.0 mm の場合は 74~76 K で 40 kPa に達した。液体窒素のサブクール度(温度)が変化した場合にも、キャビテーション発生直前と発生時のスロート静圧差から、振動圧力の大きさおよび傾向を見積ることができる。また、スロート径1.5
mm の場合、パルス的なキャビテーションが断続的に発生する流動が観測された。この流動では温度74 K で70 kPa の大きな振動圧力が確認され、下図に示すようにキャビテーション初生流速と流動時のスロート流速の動圧差から最大振動圧力の大きさを見積もることができる。
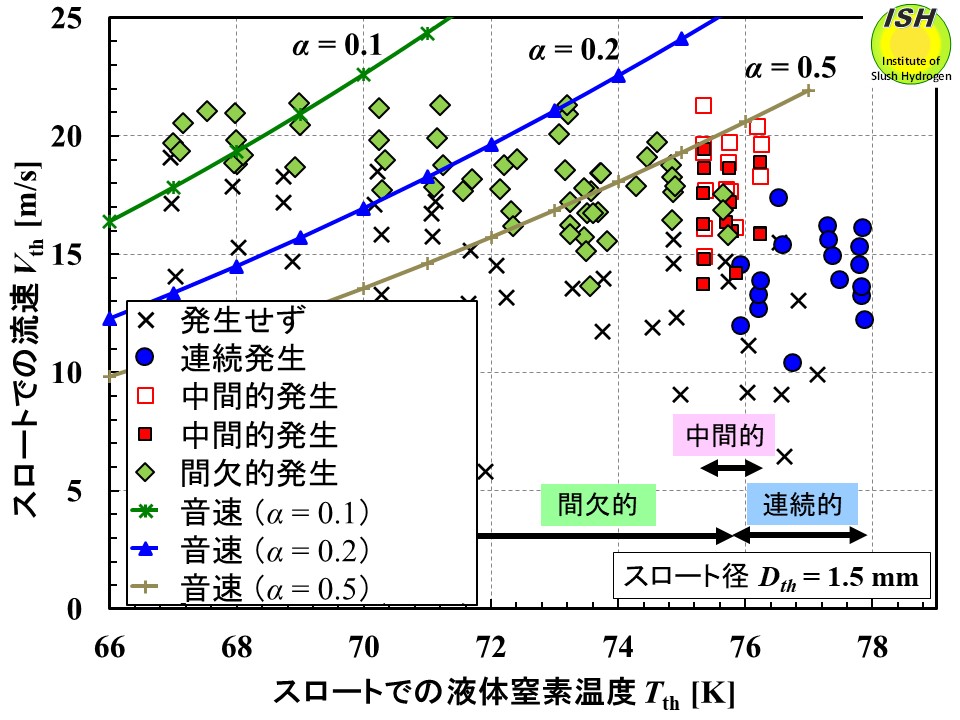
スロートでの液体窒素温度、流速、二成分系の式で計算した音速とキャビテーションモードの関係
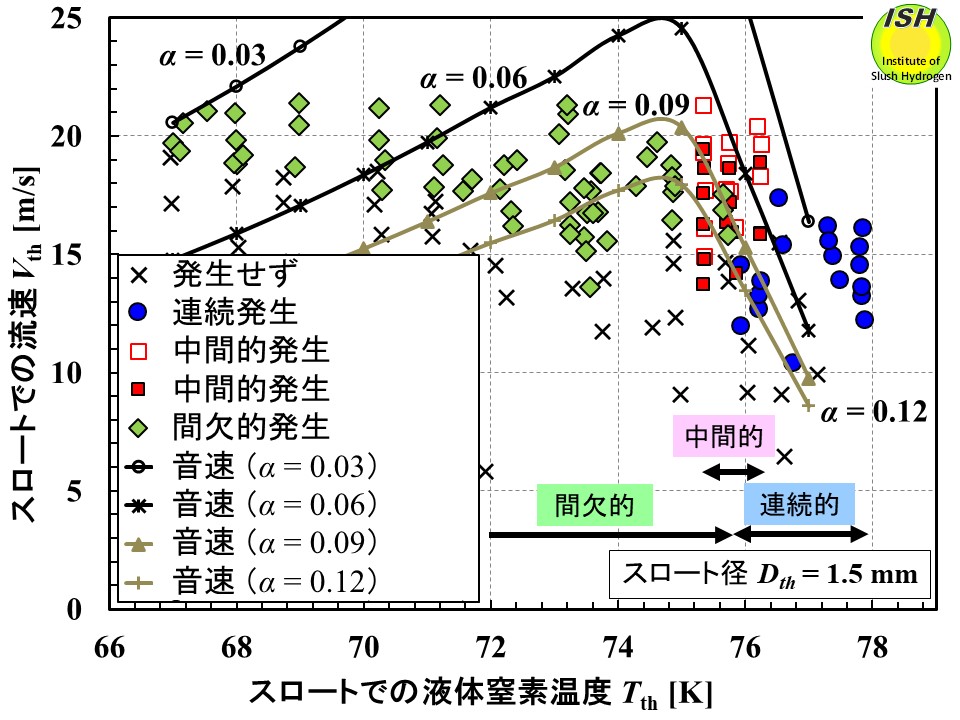
スロートでの液体窒素温度、流速、一成分系の式で計算した音速とキャビテーションモードの関係
キャビテーションモードと振動圧力