気液二相沸騰液体窒素の流動、伝熱
宇宙航空研究開発機構(JAXA)は液体水素を燃料とする極超音速機用予冷ターボジェットエンジンの開発を行っている。エンジン開発に必要となる極低温流体の気液二相状態での流動・伝熱特性はこれまで詳細に研究されていない。水平円管(内径 15 mm)を流動する沸騰液体窒素の流動パターンの可視化観察結果を上図に示す。スラグー環状流ではスラグ流と環状流の両方が、波状ー環状流では波状流と環状流の両方が現れる流動パターンである。極低温気液二相流の圧力損失および圧力変動特性、強制対流熱伝達特性、強制対流熱伝達時の流動パターンについて、研究の一部をJAXAと共同で行なった
[30, 31]。
円管(内径 10 mm、15 mm)、正方形管(一辺 12 mm)、正三角形管(一辺 20 mm)、逆正三角形管(一辺 20 mm)で得られた沸騰液体窒素の実験結果を使用して、圧力損失については
Winterton [37]、Khalil [38]、Butterworth [39]、Chisholm [47]、Levy [48]、Woldesemayat
[49]、Kadambi [50] の各式、熱伝達率については Gungor-Winterton [41]、Liu-Winterton [42]、Schrock-Grossman
[43]、Chen [44]、Kandlikar [51]、Steiner [52] の各式について評価を行った。
最後に、圧力損失-流量特性の負性勾配(d(ΔP)/dG < 0)により、圧力損失、熱伝達が周期的に大きく変動するLedinegg型流動不安定についても検討を行った。
水平正方形管内を流動する気液二相沸騰液体窒素の圧力損失と熱伝達特性
水などの常温流体を使用して、主に円管内を流動する圧力損失式および熱伝達実験式が得られているが、極低温流体の沸騰二相流の圧力損失、強制対流沸騰熱伝達に関する実験的研究は少ない。即ち、従来得られている圧力損失式および熱伝達実験式の極低温流体への適用性、円管と断面が異なる管への適用性については、これまで実験による研究が充分に行われていない。我々は、水平正方形伝熱管を流動する液体窒素沸騰二相流の流動パターンの可視化とボイド率の測定を行い、ボイド率測定結果をもとに、従来提案されているボイド率と熱平衡クオリティ(以後、クオリティと略す)の相関式を用いた圧力損失計算結果と実験結果を比較し、圧力損失モデルの評価を行った。また、クオリティおよび流動パターンの違いによる熱伝達率の違い、伝熱管上面、側面、底面における熱伝達率の違いを明らかにし、熱伝達モデルの評価を行った
[31]。
伝熱管はリン脱酸銅製の直管で、一辺d=12 mm、肉厚 1.5 mm、加熱区間 800 mmである。管外周にニクロム線を巻きつけてスタイキャストで固着しており、通電加熱した。2種類の静電容量型ボイド率計、即ち、鉛直対向平板極板タイプと水平対向平板極板タイプを設置し、LCRメータ*によるボイド率測定を行った
[14, 15]。試験条件は、ランタンク圧力Prt=0.1-0.15 MPa、質量流束G=70-2000 kg/m2-s 、熱流束q=5、10、20 kW/m2である。
実験では、気泡流(bubbly flow)、プラグ(plug)流、スラグ(slug)流、スラグー環状(slug-annular)流、波状ー環状(wavy-annular)流、波状(wavy)流の6つの流動パターンが観察された。スラグー環状流ではスラグ流と環状流の両方が、波状ー環状流では波状流と環状流の両方が現れる流動パターンである。
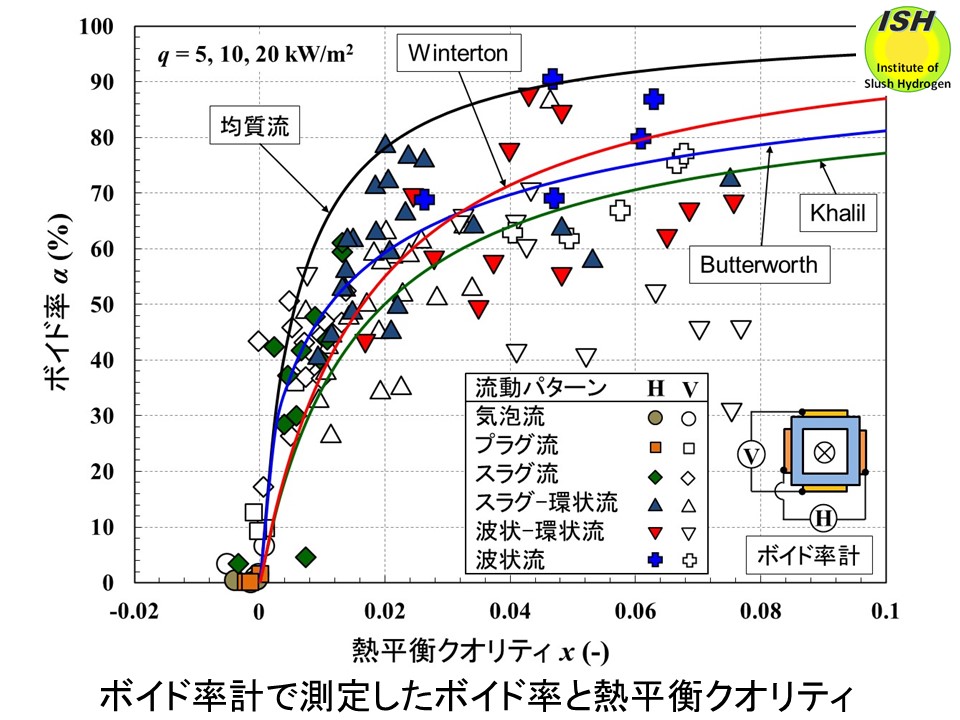
ボイド率計で測定したボイド率とクオリティの関係を下図に示す。図の実線は、均質流モデル(homogeneous flow model, スリップ比 slip ratio:s=1)と、分離流モデル(separation flow model)で提案されている Wintertonのスリップ比 [37]、Khalilのスリップ比
[38]、Butterworthモデル [39] を使用して計算した値である。クオリティが負の部分ではサブクール沸騰が発生している。高クオリティ領域では均質流モデルよりも分離流モデルの方が実験値に近い傾向を示している。鉛直対向型(vertical type: V)、水平対向型(horizontal type: H)のボイド率計では、電極を水平に取り付けた場合の方が実際のボイド率を精度良く測定している。円管の場合においても水平対向の場合が精度良く測定できるとの解析結果が報告されている [40]。
* LCRメータ:インダクタンス(L)、静電容量(C)、抵抗(R)が測定できる。 ここでは、静電容量のみを測定。
水平管の圧力損失は加速損失と摩擦損失から成る。均質流モデル(s=1)およびボイド率測定結果からボイド率を良く再現している分離流モデル(Winterton、Khalil、Butterworth)を使用して単位長さ当たりの圧力損失(ΔP/L)の計算を行った。下図は熱流束 10 kW/m2の実験で得られた圧力損失と、図中に示す代表的な実験条件で計算した均質流モデルと分離流モデルの全圧力損失、加速損失、摩擦損失を示す。参考までに液体窒素単相流の圧力損失(摩擦損失)であるブラジウス(Blasius)式を図に示す。
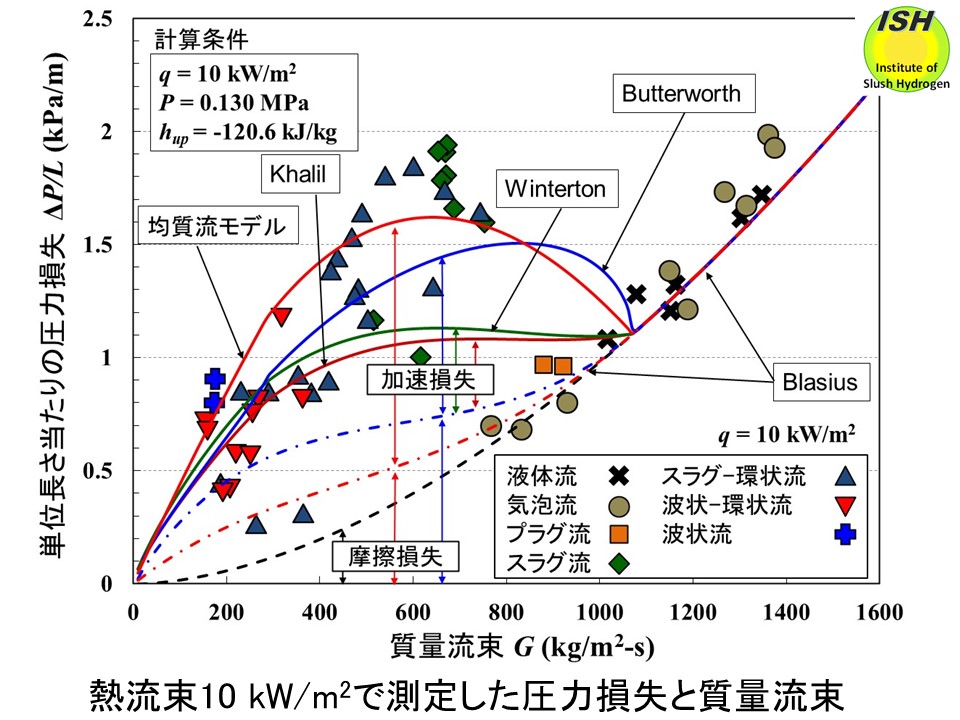
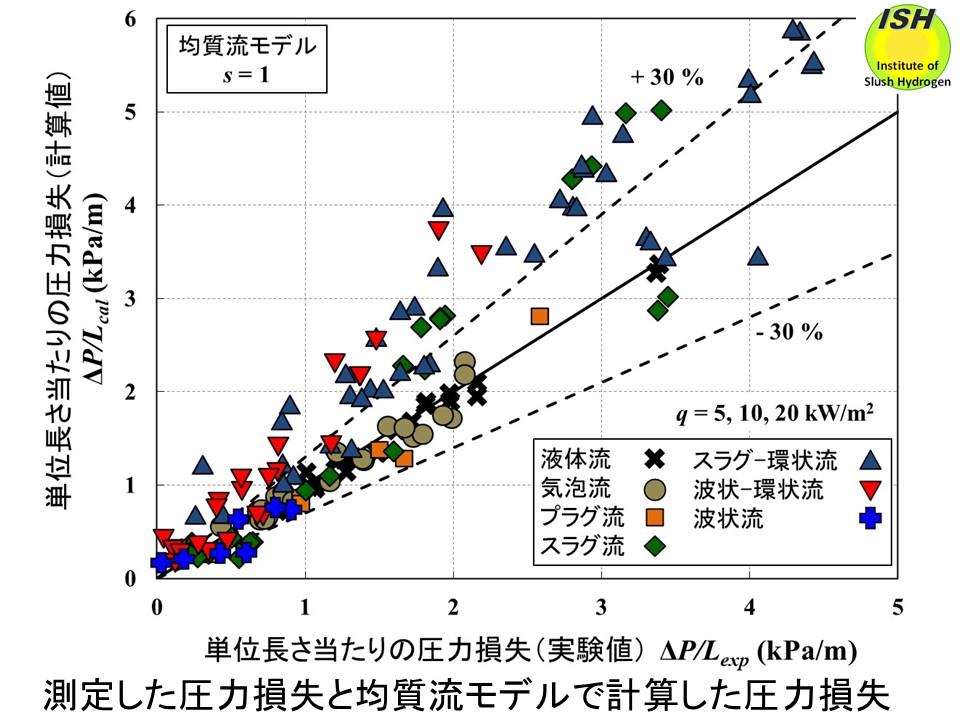
下図に熱流束 5、10、20 kW/m2で得られた圧力損失の実験結果と均質流モデル、Butterworthモデルで得られた計算結果を示す。ただし、測定区間でクオリティが負の部分については
Blasius式で計算を行っている。4種類のモデルを比較すると、均質流モデルは低ボイド率(bubbly、plug)では実験結果を評価可能であるが、圧力損失が大きい場合(高ボイド率、2
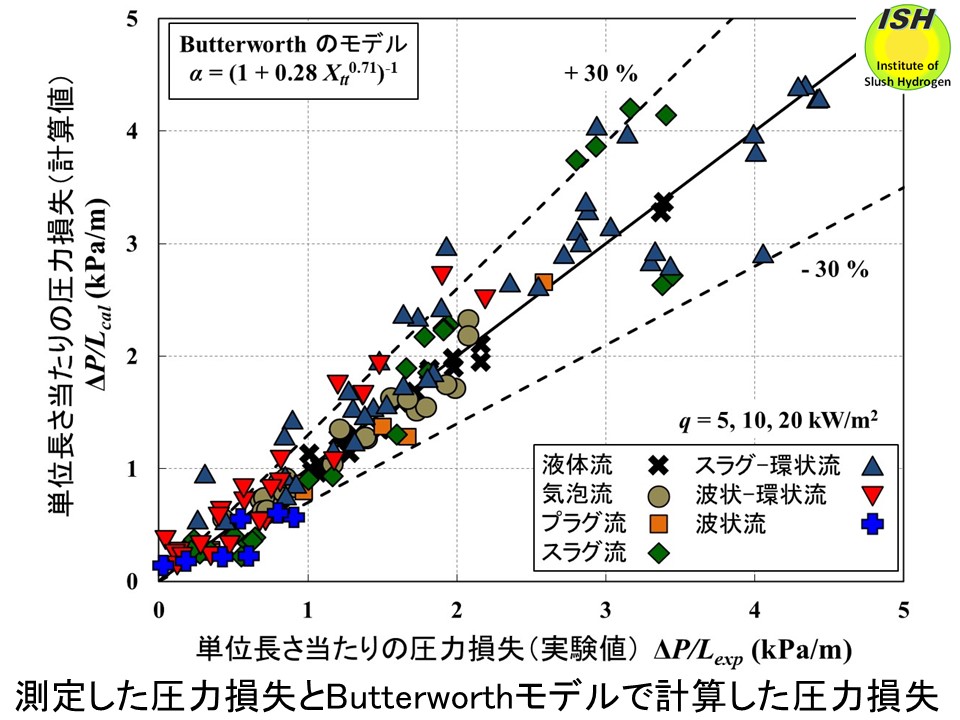
kPa/m以上)は実験値よりも30%以上大きく評価する。均質流モデルでは液相と気相の流速が同じと仮定しているため、液相の流速を大きく見積もっており、その結果、圧力損失を大きく見積もっている。Butterworthモデルの計算結果では、下図に示すように殆ど全ての流動様相において大部分の実験値を±30%以内で評価している。実験値と計算値を絶対平均偏差で評価すると Butterworthモデルの方が良い結果となった。Winterton、Khalilの式を用いた場合も大部分の実験値を±30%以内で評価可能であり、分離流モデルの方が実験結果を良く評価している。
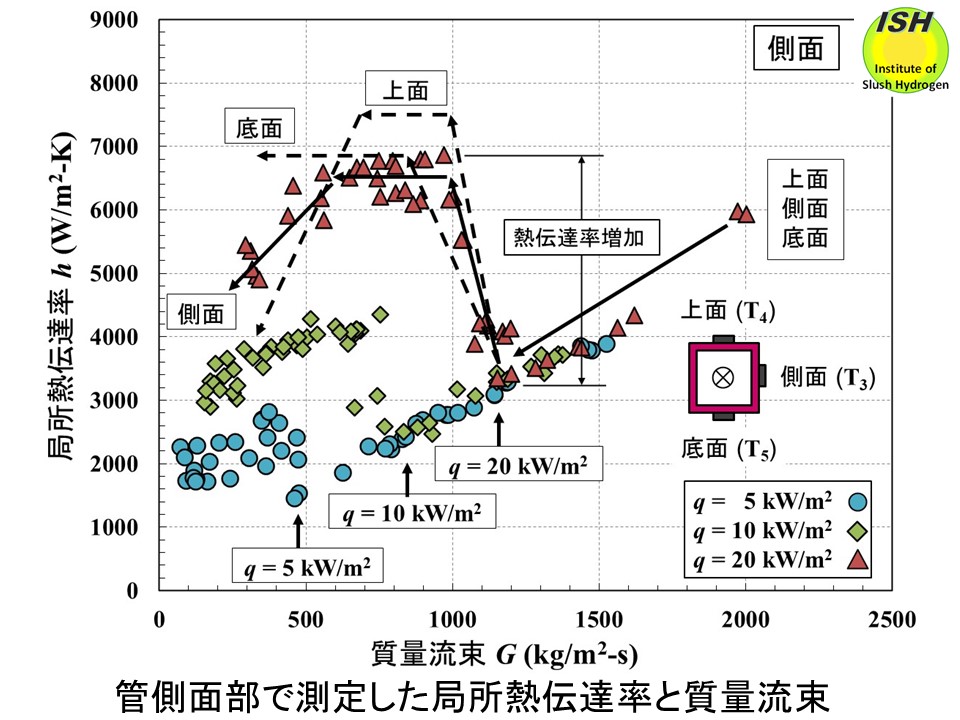
下図に熱流束q=5、10、20 kW/m2の場合の管側面(T3)の熱伝達率を示す。質量流束が大きい領域では液単相強制対流熱伝達が支配的であり、熱伝達率は熱流束に依存せず、質量流束の大きさに依存する。また、高質量流束域では側面、上面、底面で熱伝達率の差は殆ど認められなかった。実線の矢印で示すように、質量流束が小さい領域では、質量流束が低下すると沸騰が開始し熱伝達率が増加する。さらに質量流束が低下すると核沸騰熱伝達が支配的となり、熱伝達率はある一定値まで増加する。沸騰が開始する質量流束点(qの値を図示)は熱流束が小さいほど小さくなり、熱伝達率の増加量は熱流束が大きいほど大きくなる。
図には熱流束 20 kW/m2時の側面の核沸騰熱伝達率を実線で、上面、底面を破線で示している。底面では質量流束の低下に伴い熱伝達率は増加して一定値まで達した後、低質量流束域まで維持される。核沸騰熱伝達が支配的となり、質量流束の大きさに依存せず、熱流束の大きさに依存して熱伝達率が一定となっている。上面では質量流束の低下に伴い側面や底面よりも熱伝達率は増加するが、さらに低質量流束になると減少する。即ち、沸騰により発生した気泡は上面に集中して流れるため熱伝達が促進され、熱伝達率が増加する。さらに質量流束が低下すると壁面がドライアウトして熱伝達率が低下する。側面では底面と同様な挙動を示すが、ドライアウトが発生すると熱伝達率が低下し始める。上面に比べ低質量流束域でも液相が存在し、核沸騰熱伝達が維持されるため熱伝達率低下が起こり始める質量流束点が小さく、低下割合も緩やかである。
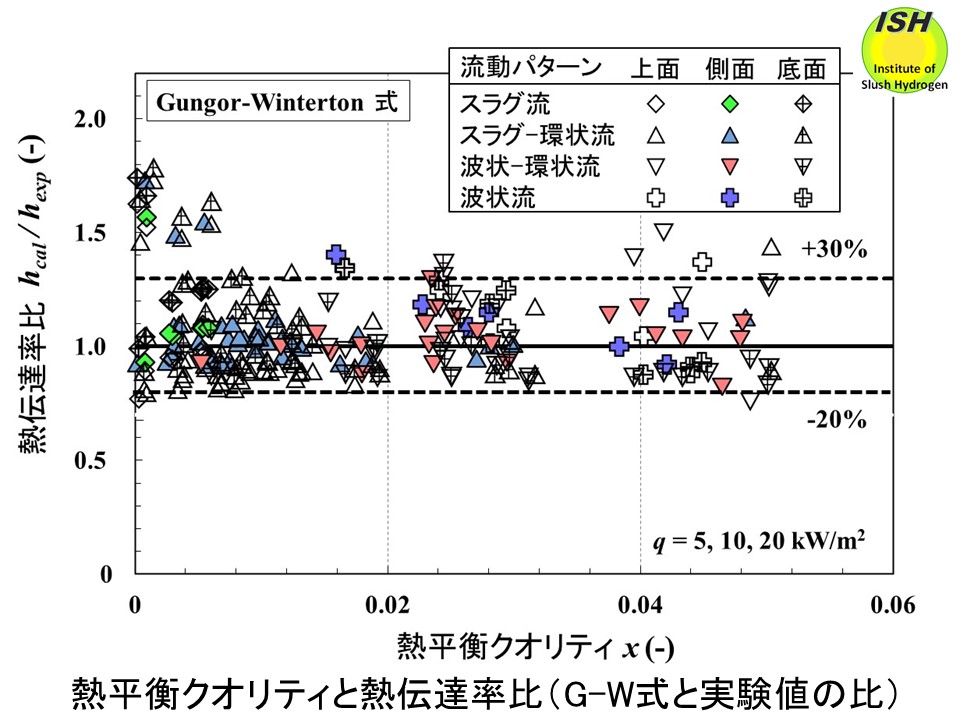
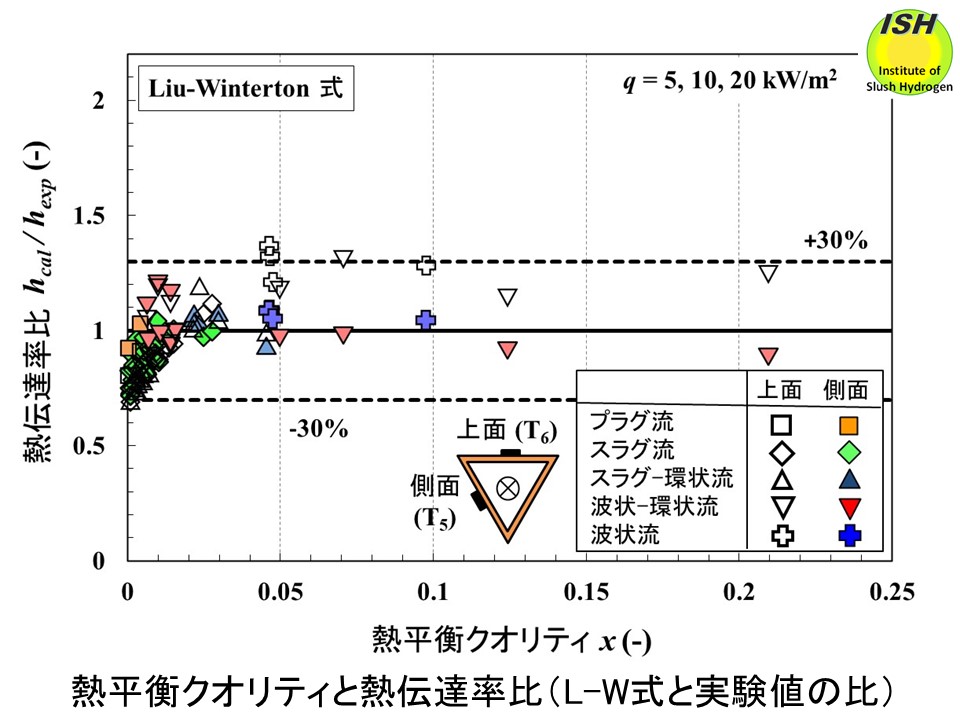
管側面、上面、底面の熱伝達率を水等の常温流体で提案されている気液二相の熱伝達式である Gungor-Winterton式 [41] とLiu-Winterton式
[42] で評価した結果を示す。測定部でクオリティがゼロもしくは負の場合、流動パターンは液単相流、気泡流、プラグ流が観察され、測定部の周方向位置によらず
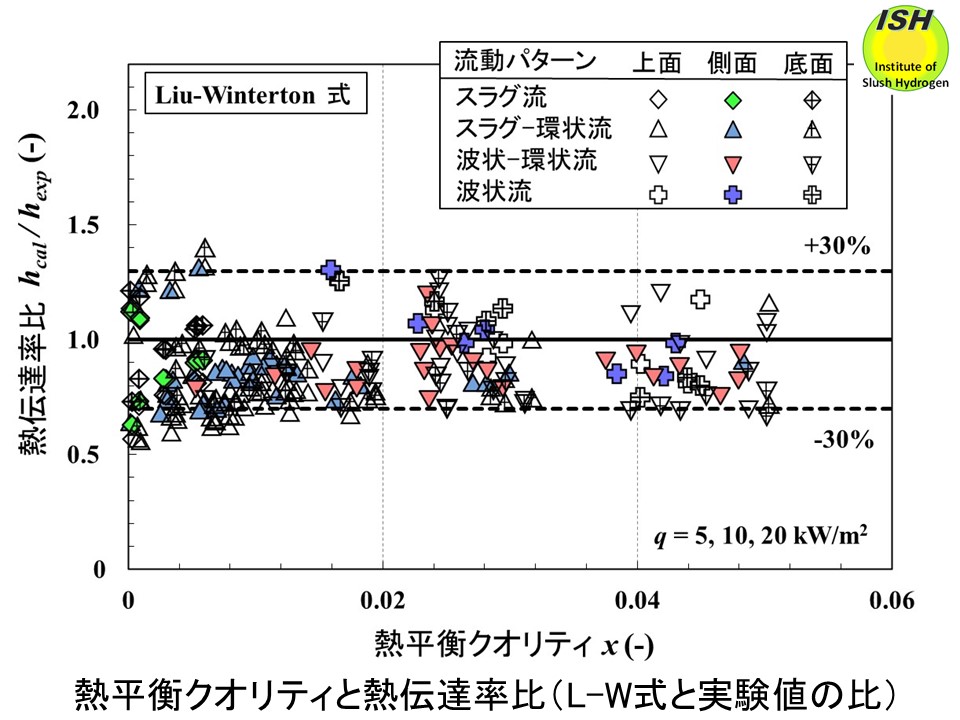
Dittus-Boelter式でおよそ±20%で評価可能である。測定部でクオリティが正の場合、スラグ流、環状流、波状流が観察され、次の結果が得られた。下図に Gungor-Winterton式との比較を示す。クオリティが 0.006 以上で測定部の周方向位置によらず実験値の大部分を+30%~-20%で評価可能である。下図に示す Liu-Winterton式は Gungor-Winterton式よりも実験値を小さく評価する傾向があるが、クオリティが小さい領域でも実験値との差は小さく、実験値の大部分を±30%以内で評価可能である。実験値と計算値を絶対平均偏差で評価すると
Gungor-Winterton式の方が実験結果を良く評価している。
水平三角形管内を流動する気液二相沸騰液体窒素の圧力損失と熱伝達特性
高温超伝導機器の実用化と共に、冷媒としての液体窒素の重要性は今後益々高まると予想され、機器の予冷時、超伝導線のクエンチ時に液体窒素は気液二相沸騰状態となるため、流動時の圧力損失と強制対流沸騰熱伝達特性が機器の設計上重要となる。高温超伝導機器には、種々の断面形状をもつ冷媒配管や熱交換器の使用が予想され、管内を流動する極低温流体の流動、伝熱特性が重要となる。三角形管は、同一水力直径の円管と比較すると、伝熱面積が増加すると共に集積性にも優れており、三角形断面形状はプレートフィン熱交換器等にも利用されている。
一辺 20 mmの水平正三角形管を流動する液体窒素沸騰二相流の流動、伝熱試験を実施し、流動パターンの可視化、ボイド率、圧力損失、熱伝達率の測定を行った。ボイド率測定結果をもとに、従来提案されているボイド率と熱平衡クオリティ(以後、クオリティと略す)の相関式を用いた圧力損失計算結果と実験結果を比較し、圧力損失モデルの評価を行った。また、流動パターンによる熱伝達特性の違い、管側面、管底面における熱伝達特性の検討を行い、熱伝達式モデルの評価を行った
[46]。
長さ 800 mm、一辺 20 mmの無酸素銅製正三角形管の外壁にニクロム線ヒータをスタイキャストで固着し加熱した。圧力損失は加熱区間550 mmで測定し、流れ方向6点で測定した外壁温度から解析的に計算した内壁温度と測定したバルク(流体)温度から局所熱伝達率を算出した。管側面(T5)、管底面(T6)の局所熱伝達率を評価する。伝熱部下流には二重螺旋型の静電容量型ボイド率計、可視化管を設置している。試験時の伝熱管入口圧力 0.11-0.15
MPa、質量流束G=110-2370 kg/m2-s、熱流束q=5、10、20 kW/m2である。
気泡流、プラグ流、スラグ流、スラグー環状流、波状ー環状流、波状流の6種類の流動パターンが観察された。
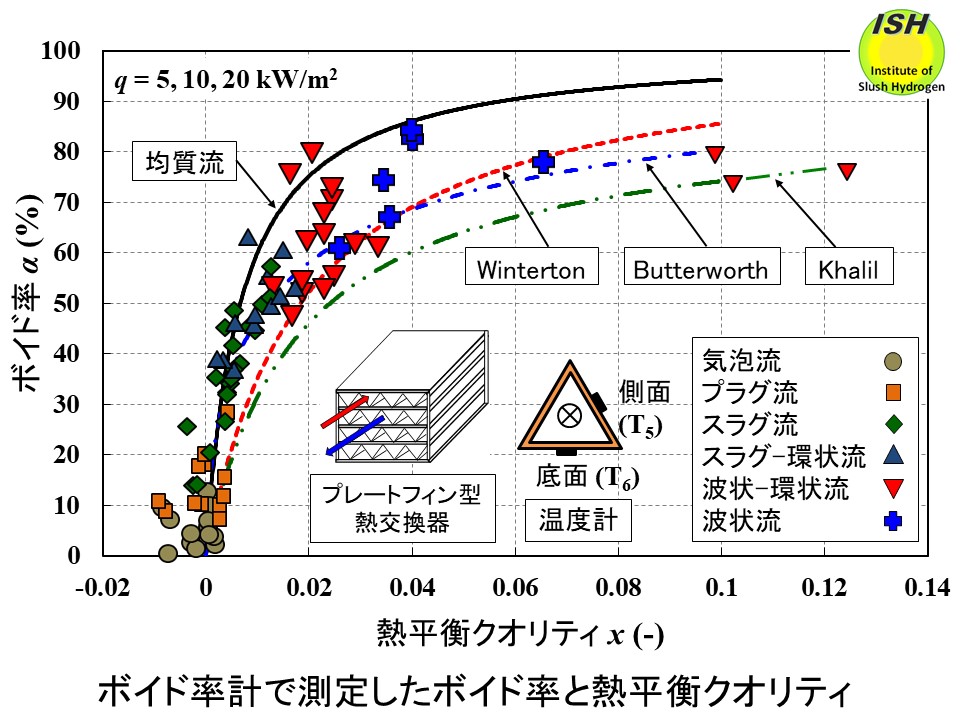
下図は測定したボイド率とクオリティの測定結果を示す。伝熱管入口で液体窒素が若干のサブクール状態であるため、クオリティが負 の部分(x< 0)ではサブクール沸騰が発生している。後述の圧力損失評価において、分離流モデルでは加速損失の見積りにボイド率が必要になるためボイド率とクオリティの関係式が見積り精度に大きく左右される。図には均質流(homogeneous
flow)モデル(スリップ比s=1)と分離流モデルで提案されている Winterton、Khalilのスリップ比 [37, 38]、Butterworthモデル [39]
を使用したボイド率とクオリティの関係を示す。我々の従来の実験結果では二重螺旋型ボイド率計の測定値は実際よりも大きな値を示す傾向があり、後述のように、Khalilのスリップ比を使用した圧力損失モデルが実験結果と良い一致を示した。均質流モデルは実際のボイド率を過大評価している。
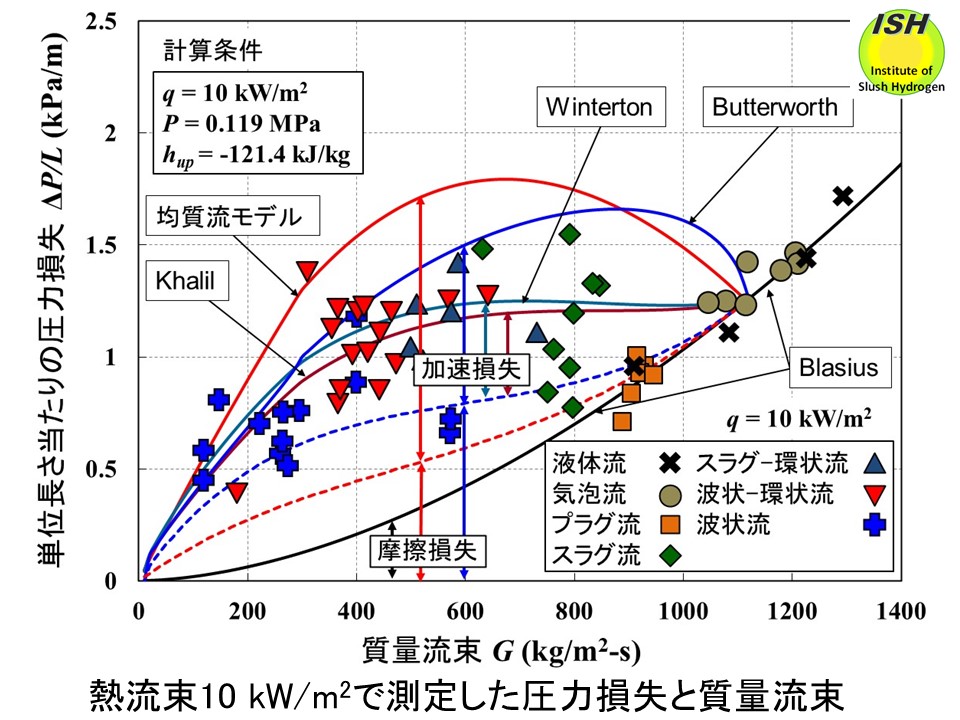
水平管の圧力損失は加速損失と摩擦損失から成る。均質流モデル(s=1)およびボイド率測定結果からボイド率を良く再現している分離流モデル(Winterton、Khalil、Butterworth)を使用して単位長さ当たりの圧力損失(ΔP/L)の計算を行った。下図は熱流束 10 kW/m2の実験で得られた圧力損失と、図中に示す代表的な実験条件で計算した均質流モデルと分離流モデルの全圧力損失、加速損失、摩擦損失を示す。参考までに液体窒素単相流の圧力損失(摩擦損失)であるブラジウス(Blasius)式も図に示す。
従来の圧力損失評価モデルは円管を流動する常温流体の実験結果をベースにしており、液体窒素へ適用した報告例は少ない。本実験では、ランタンクを若干加圧して伝熱管へ圧送しているため、実験条件により、圧力損失測定区間のクオリティが負(x< 0)、正(x> 0)もしくは負と正が混在する場合がある。全て負(x< 0)の場合、サブクール沸騰の影響が大きくなると(可視化部でスラグ流、スラグー環状流に相当)、ブラジウス式は実験値を30%以上小さく評価した。ボイリング数をパラメータとする修正ブラジウス式を提案して評価した結果、サブクール沸騰時の圧力損失をおよそ±20%以内で予測できる結果を得た。
圧力損失測定区間のクオリティが正(x> 0)、もしくは負と正が混在する二相流の圧力損失計算においては、サブクール区間(x< 0)では摩擦損失を従来のブラジウス式で評価し、二相流区間(x> 0)では、前述の4種類のモデル(Homogeneous、Winterton、Khalil、Butterworth)で評価した。
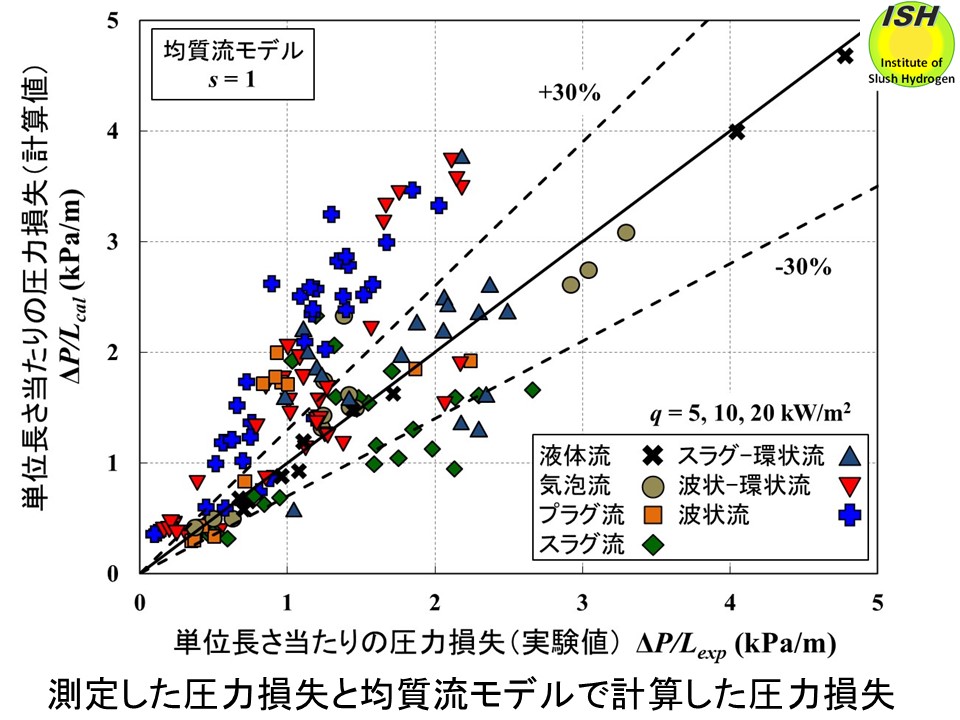
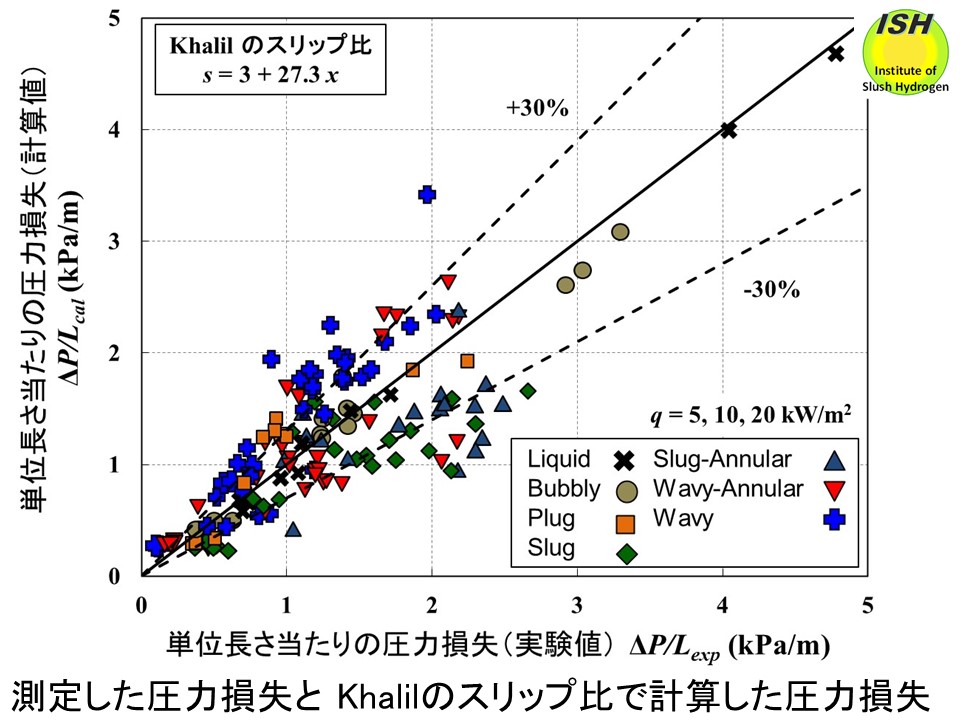
下図に熱流束 5、10、20 kW/m2で得られた圧力損失の実験結果と均質流モデル、Khalilモデルで得られた計算結果を示す。計算値と実験値の比較を行った結果、Khalilモデルが実験値と良い相関を示した。
熱流束 5、10、20 kW/m2において、熱伝達率測定位置のクオリティが負(x< 0)で、サブクール沸騰の影響が大きい場合(可視化部で slug flow、slug-annular flowに相当)は、気泡発生により側面、底面共に
Dittus-Boelter式は実験値を30%以上小さく評価した。圧力損失の場合と同様に、ボイリング数をパラメータとする修正Dittus-Boelter式を提案して評価した結果、サブクール沸騰時の熱伝達率をおよそ±15%以内で予測できる結果を得た。
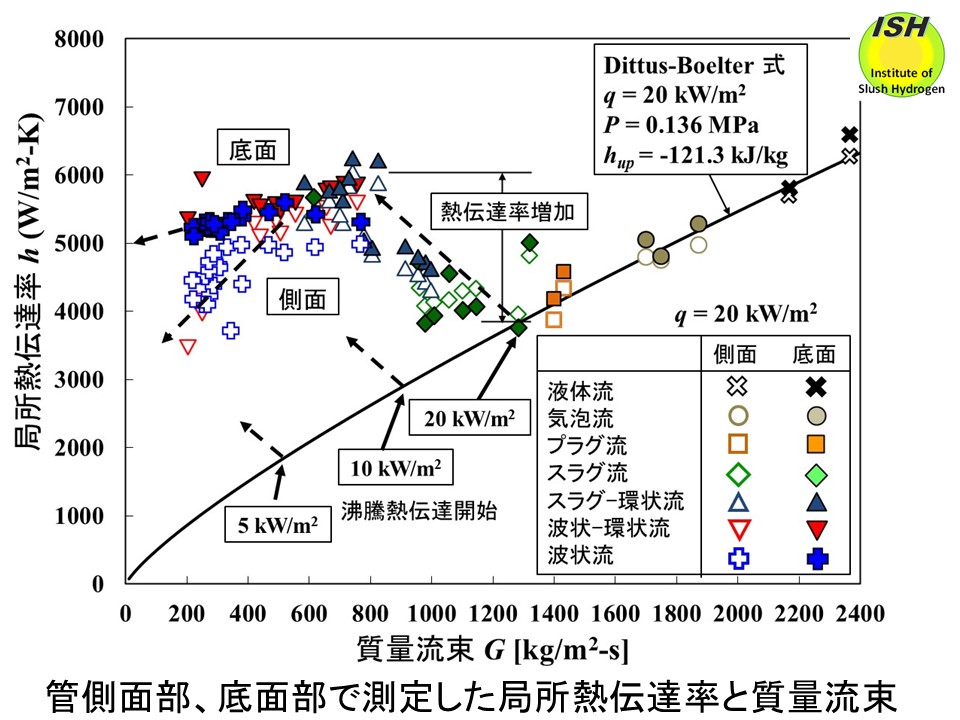
熱流束 20 kW/m2での質量流束Gと熱伝達係数hの実験結果を下図に示す。図中の従来の Dittus-Boelter式は代表的な実験条件を使用して計算している。サブクール沸騰状態では液単相強制対流熱伝達が支配的であり、側面、底面で熱伝達率の差は小さい。飽和二相流(x> 0、G< 1300 kg/m2-s)の場合、管底面では質量流束の低下に伴い熱伝達率は増加して一定値まで達した後、低質量流束域まで一定に維持され、その後、緩やかに低下する。側面では質量流束の低下に伴い、核沸騰および発生した気泡により熱伝達が促進されるため底面よりも熱伝達率は増加する。さらに低質量流束になると壁面が一部ドライアウトして熱伝達率は大きく低下する。
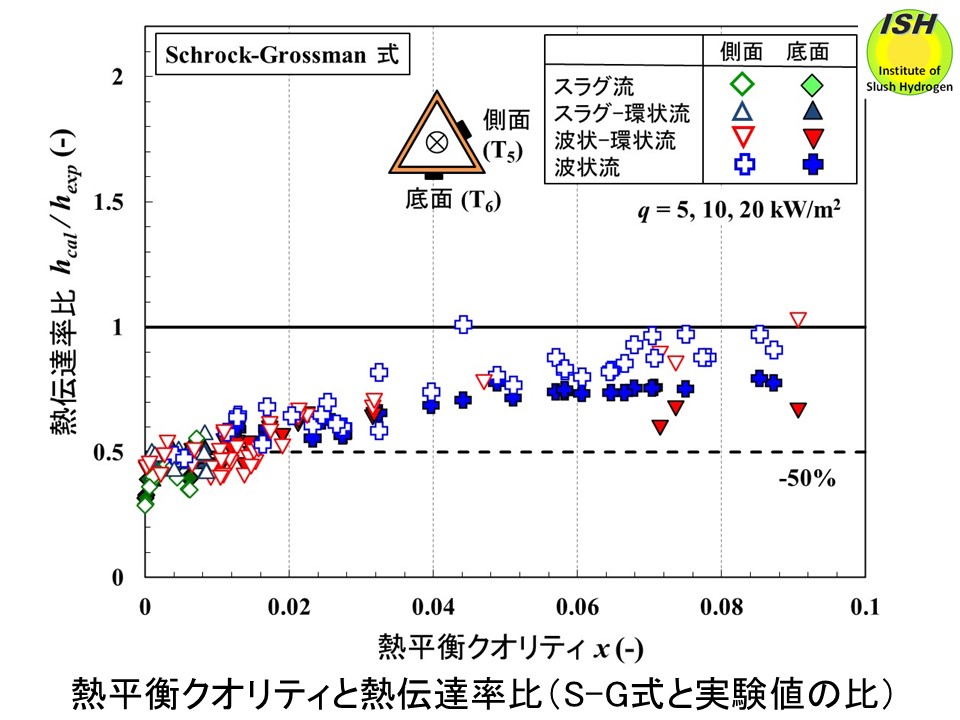
側面、底面で測定した熱伝達率をもとに4種類の熱伝達式 Schrock-Grossman [43]、Chen [44]、Gunger-Winterton
[41]、Liu-Winterton [42] を定量的に比較した結果を示す。
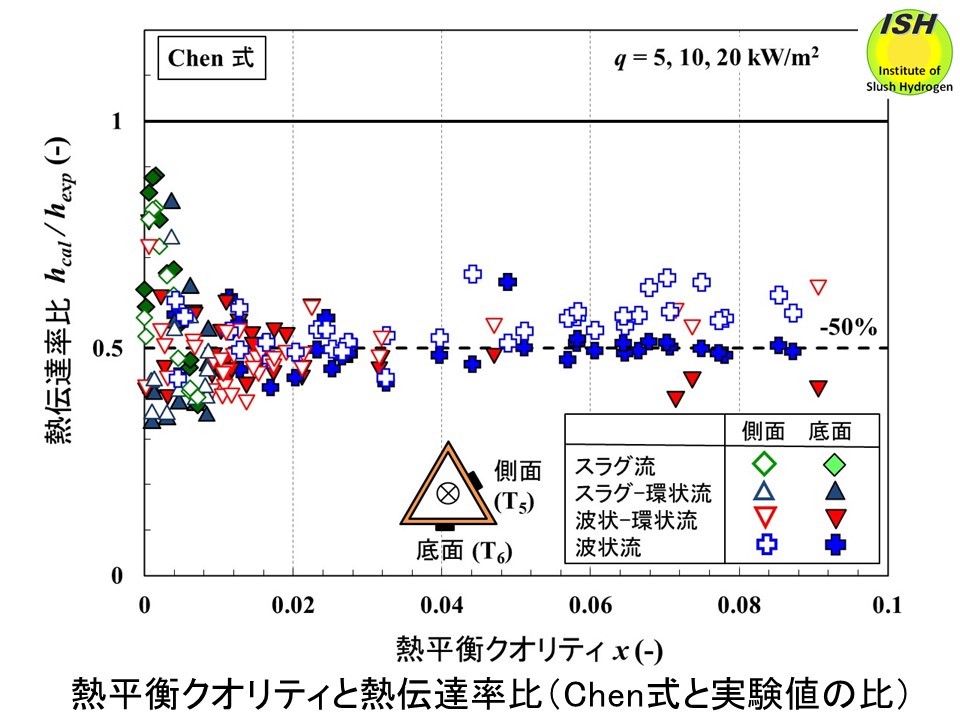
下図に示す Schrock-Grossman式の場合、クオリティが小さい(x< 0.02)領域では計算値は実験値の50%程度の小さい値を示しており、クオリティが大きくなると0-30%程度小さい値となる。クオリティがさらに大きくなると(x> 0.09)、計算値と実験値が良く一致すると考えられる。下図に示す Chen式の場合、実験を行った全てのクオリティ(0 <x< 0.09)において、計算値は実験値の50%程度の小さい値を示している。Schrock-Grossman式は水を対象にした実験式であり、Chen式は水、メタノール等を対象にした実験式である。いずれも鉛直管を使用して得られた実験データを基にしており、本実験では水平管であるため、伝熱管の姿勢が実験データを小さく評価する理由の一つと考えられる。
Schrock-Grossman式および Chen式の場合、我々が実施した内径15 mmの水平円管(0 <x< 0.07)[45]、一辺12 mmの水平正方形管(0 <x< 0.055)の実験(q=5, 10, 20 kW/m2)[31] においても同様な結果が得られている。Schrock-Grossman式および Chen式は実験値を50-60%程度小さく見積もる結果が得られた。
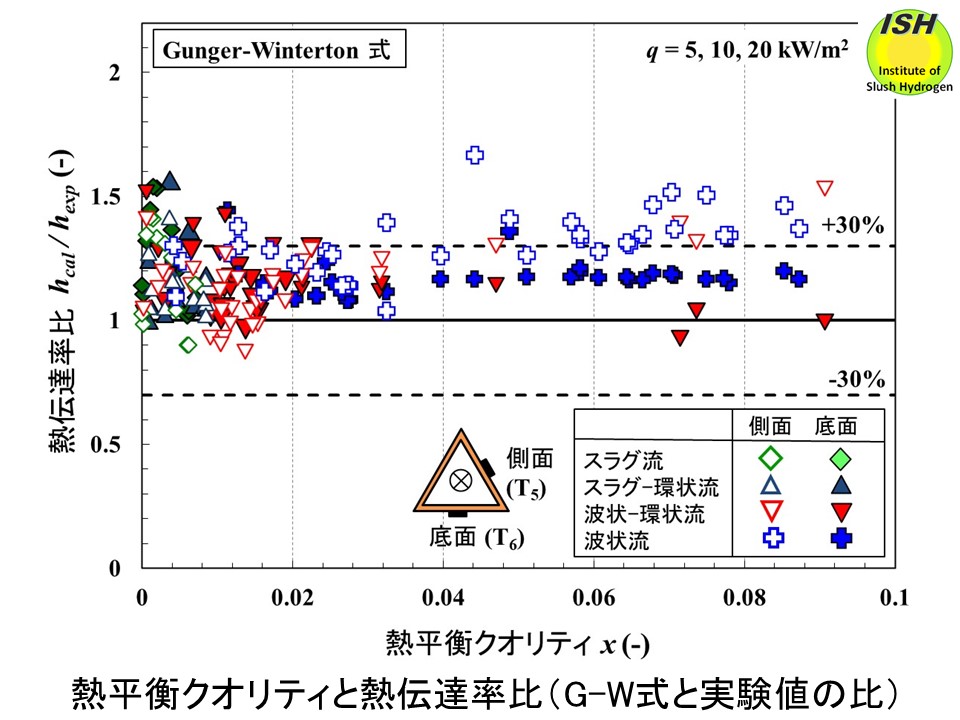
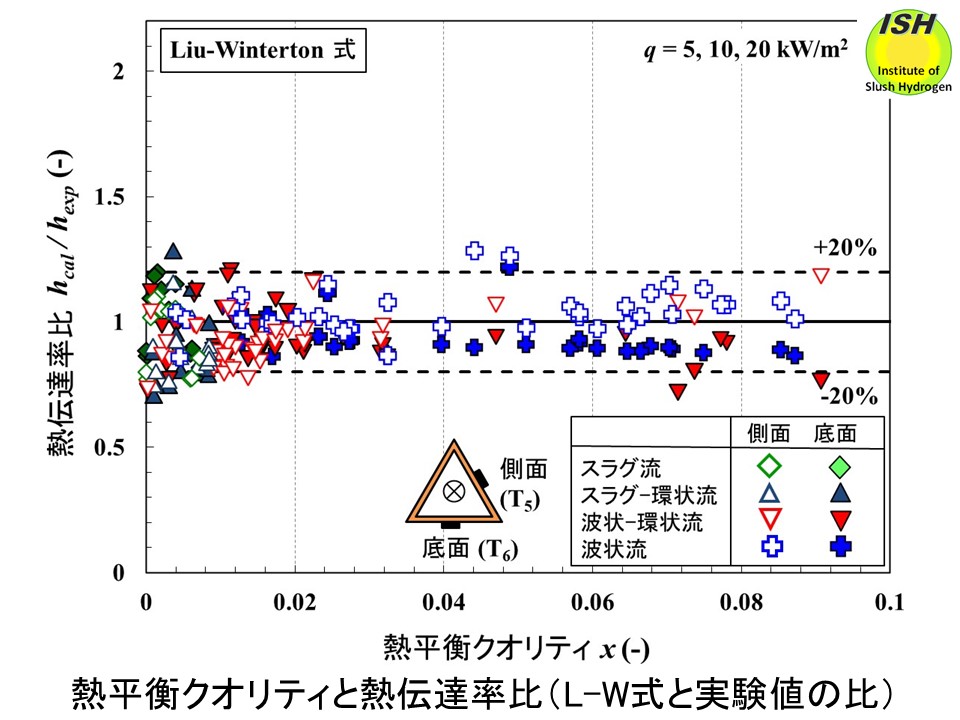
下図に示す Gunger-Winterton式の場合、熱平衡クオリティx> 0.006で管底面の熱伝達率の大部分を0-20%で評価可能である。管側面ではクオリティが大きくなり(0.04 <x< 0.09)、波状流となると壁面において部分的にドライアウトが発生し、実験で得られた熱伝達が低下する。このため、相関式は熱伝達率を30-50%程度過大評価する。下図に示す Liu-Winterton式の場合、Gungor-Winterton式よりも実験値を小さく評価する傾向があるが、熱平衡クオリティが小さい領域においても実験値との差は小さく、実験を行った全てのクオリティ(0
<x< 0.09)において、計算値は実験値の±20%程度で良い一致を示している。絶対平均偏差、標準偏差の点からもLiu-Winterton式の方が実験値を良く評価している。
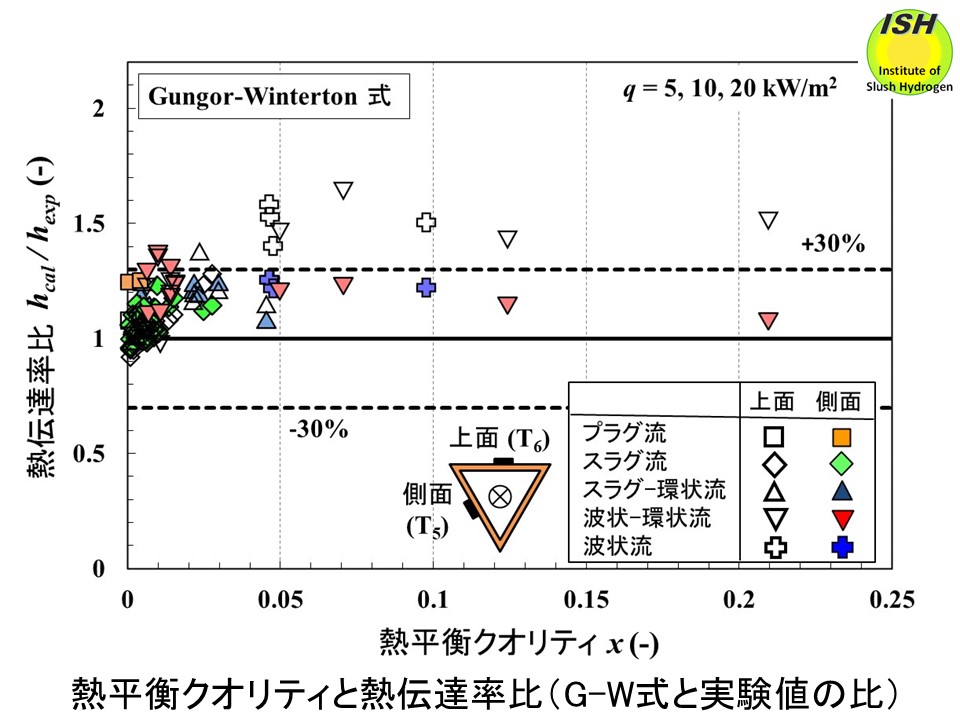
水平逆三角形管の熱伝達率の測定結果と Gunger-Winterton式、Liu-Winterton式の比較結果を下図に示す。管上面ではクオリティが大きくなり(x> 0.05)、波状流となると壁面において部分的にドライアウトが発生し、実験で得られた熱伝達率が低下する。即ち、相関式は熱伝達率を過大評価する。
気液二相沸騰液体窒素の管内流で発生するLedinegg型流動不安定
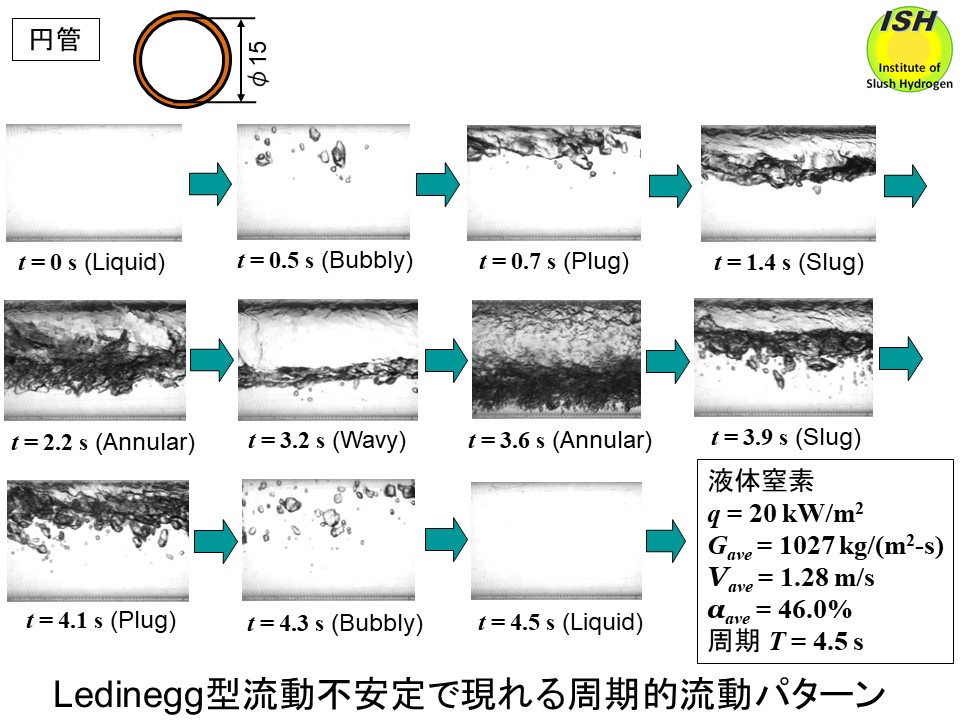
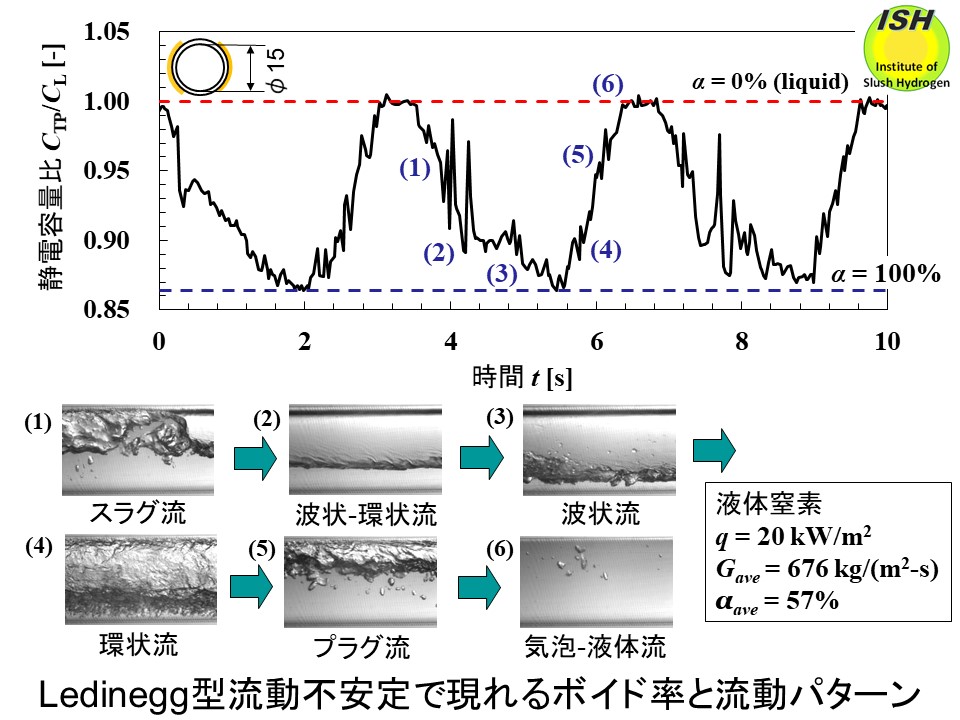
管内を流動する沸騰気液二相流では、圧力損失-流量特性の負性勾配(d(ΔP)/dG < 0)が原因でLedinegg型流動不安定が発生する。水平円管(内径 15 mm)を流動する沸騰液体窒素の流動パターンが周期的に変化する可視化観察結果を上図に示す。
Ledinegg型流動不安定の発生メカニズムを下図にまとめた。
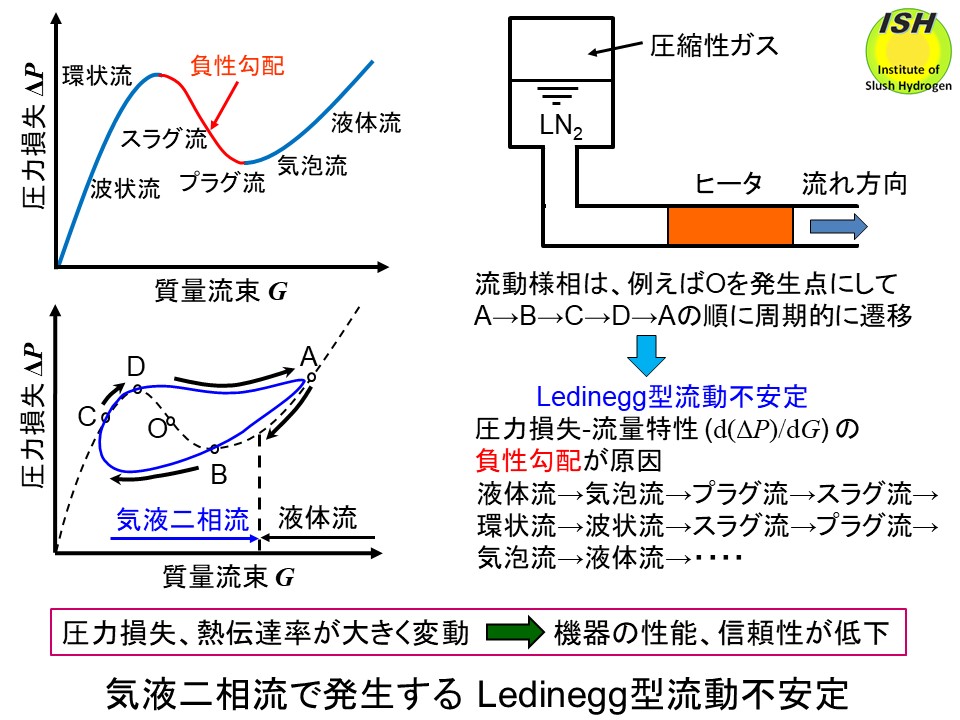
流動不安定が発生すると圧力損失、熱伝達率が大きく変動するため、極低温機器の性能低下、機器の破壊など重大な事故を発生することが考えられる。水平円管(内径
15 mm)を流動する沸騰液体窒素のボイド率と流動パターンが周期的に変化する測定結果、可視化観察結果を下図に示す。
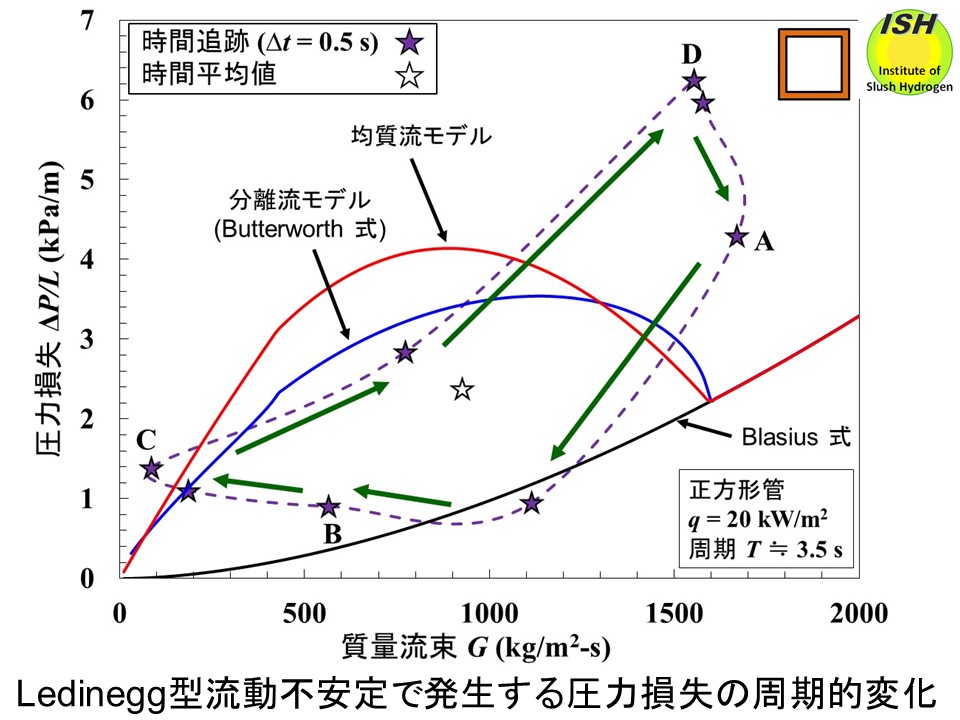
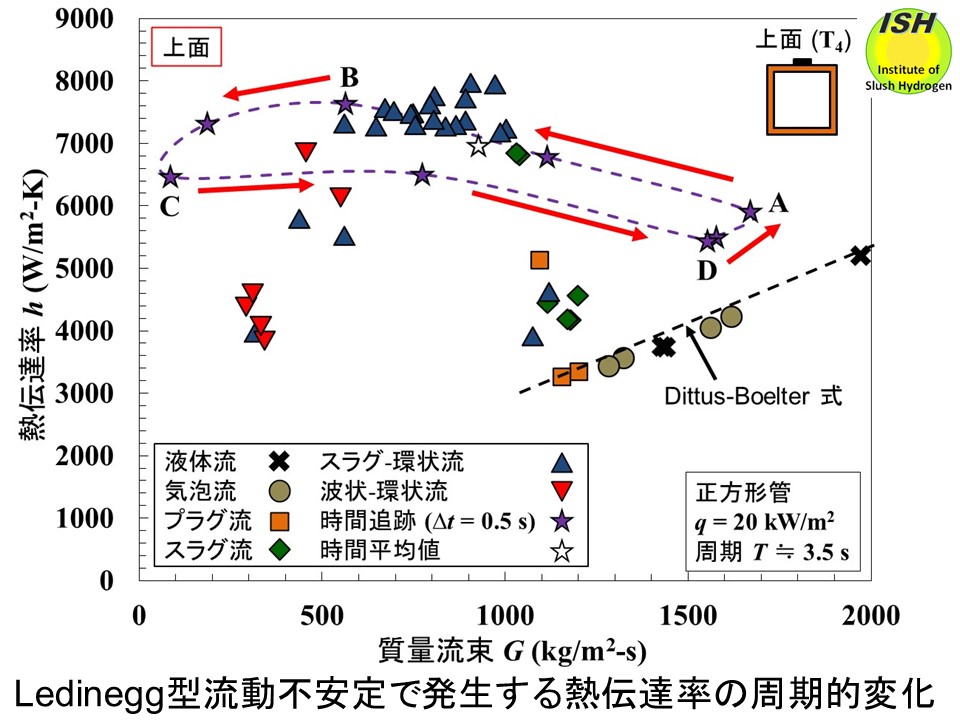
一辺 12 mmの水平正方形管の実験で得られた圧力損失、熱伝達率の変動を下図に示す。内径 15 mmの水平円管、一辺 20 mmの水平正三角形管、一辺 20 mmの水平逆三角形管の実験においても Ledinegg型流動不安定
の発生を確認し実験データを得ている。