スラッシュ水素、スラッシュ窒素のプール核沸騰熱伝達

　貯蔵した液体水素もしくはスラッシュ水素を高温超伝導マグネットの冷媒として使用する場合、プール核沸騰熱伝達特性が重要となる。

　直径 0.025 m の銅製円型伝熱面の向きを変えて（上向き、横向き、下向き）、大気圧液体水素（0.1 MPa、20 K：LH₂at NBP)、三重点液体水素（0.007 MPa、14 K：LH₂at TP)、三重点スラッシュ水素（0.007 MPa、14 K：SLH₂at TP）の核沸騰熱伝達率を測定した [28]。実験での固相率は 20-35 wt.%であり限界熱流束（CHF）も測定している。また、液体窒素、スラッシュ窒素の熱伝達率も同様に測定している。

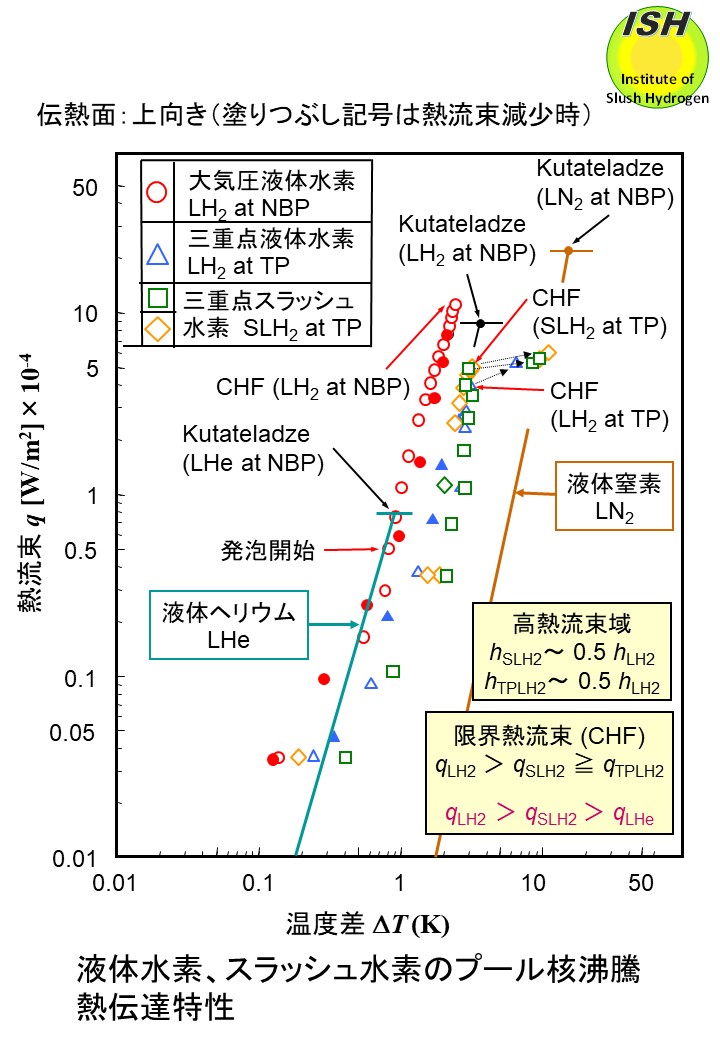
　上図は伝熱面が上向きの場合の大気圧液体水素、三重点液体水素、三重点スラッシュ水素の熱流束　q、伝熱面との温度差（過熱度）ΔTを示す。熱伝達率　h＝q/ΔTである。また、上向き伝熱面に適用される Kutateladze 式から算出した液体水素、液体窒素、液体ヘリウムの限界熱流束　q*を図に示している。

　大気圧液体水素の熱伝達率は液体ヘリウムと同程度である。スラッシュ水素の高熱流束域での熱伝達率は大気圧液体水素の約 0.5倍に低下する。

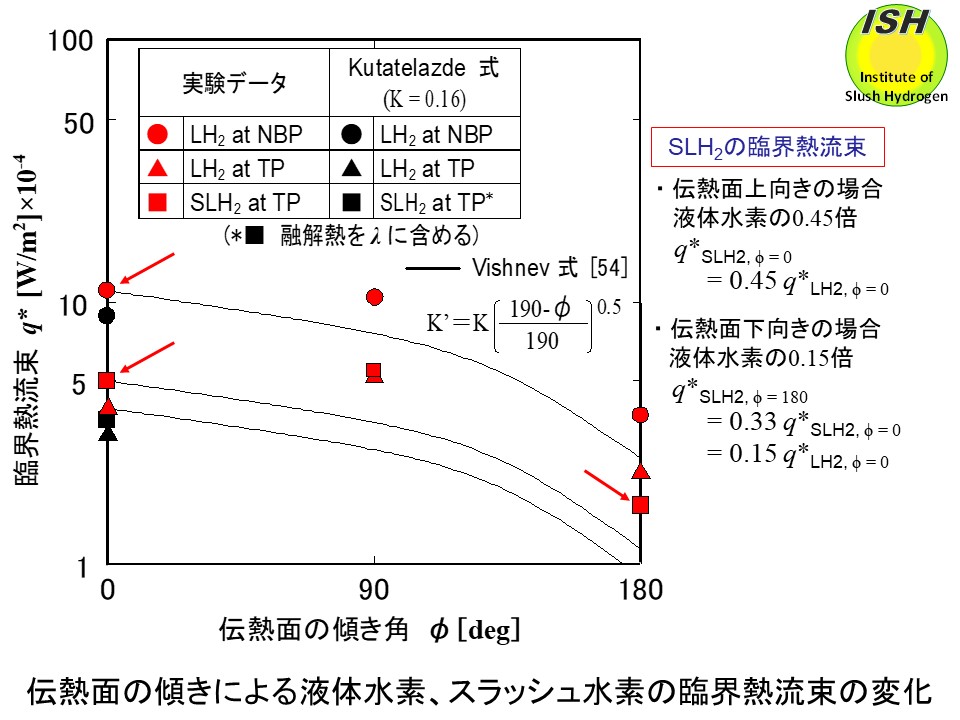
　スラッシュ水素の限界熱流束は上向き伝熱面の場合、大気圧液体の 0.45倍となり、下向き伝熱面の場合、さらに低下して大気圧液体の 0.15倍となる。すなわち、大気圧液体水素の限界熱流束　q*＝11 W/cm²（ΔT＝ 2 K）はスラッシュ水素の限界熱流束　q*＝5 W/cm²（ΔT＝3 K）、液体ヘリウムの限界熱流束　q*＝1 W/cm²（ΔT＝1 K）よりも高い限界熱流束を持っている。

　遠隔地にパイプライン輸送したスラッシュ水素は輸送時の侵入熱により固体水素粒子が融解するので液体水素の形態で貯蔵することが予想され、電力貯蔵（SMES）用高温超伝導マグネットの冷媒として大気圧液体水素を利用する方が伝熱特性上有利となる。

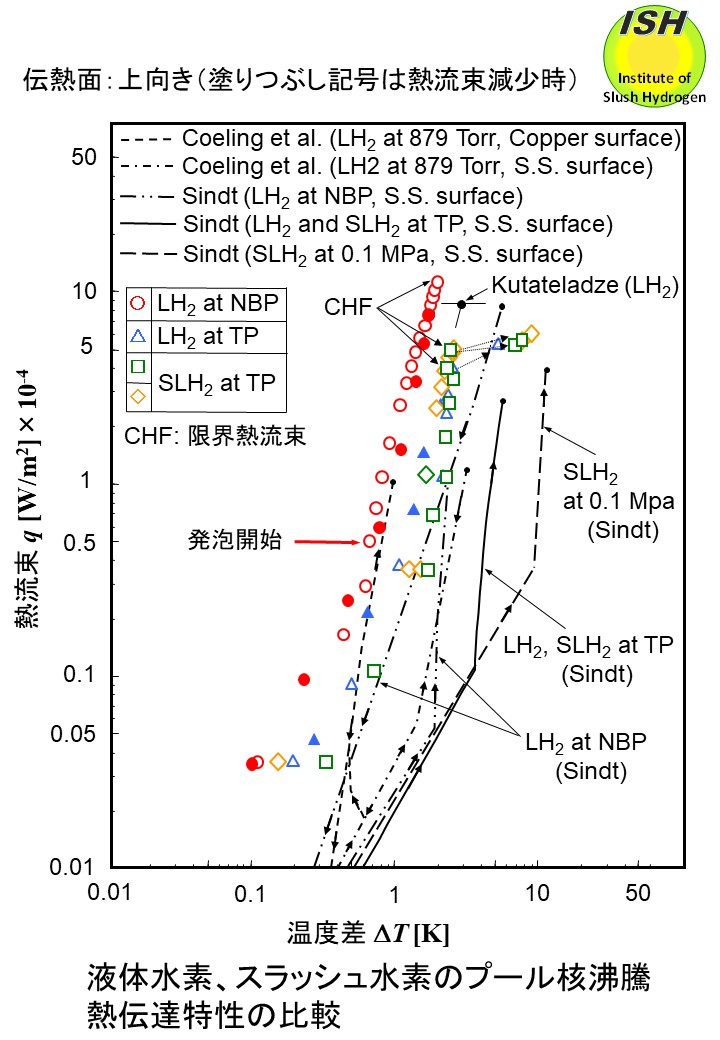
　Coeling ら [58] が液体水素中で直径 0.0254 mm の平板伝熱面（伝熱面表面粗さ 0.13 μm）で得た結果を伝熱面が銅とステンレス鋼の場合を下図に示す。また、図には Sindt [59] が直径 0.0254 m のステンレス鋼製伝熱面（表面粗さ不明）で得た結果と本実験で得られた銅製伝熱面（伝熱面表面粗さ 0.2 μm）の結果を示す。Sindt の実験では、固相率45 wt.%であり、ヘリウムガスで加圧した大気圧スラッシュ水素（0.1 MPa）の熱伝達も測定している。また、伝熱面が上向き、横向き、下向きの場合について、自然対流領域から核沸騰領域まで熱流束が比較的小さい領域での熱伝達特性を取得しており、実用上重要となる熱流束が大きい領域から限界熱流束点（CHF）までの特性が確認されていない。
　本実験で得られた大気圧液体水素の核沸騰領域での結果は Coeling らの銅製伝熱面の結果と同じ傾向を示しており、Sindt の沸騰曲線の傾向についても本実験結果とよく似ており、温度差の大きい方にずれているのは、伝熱面の材質と表面性状（粗さ）の違いによるものと考えられる。
　Sindt の実験では核沸騰領域において伝熱面の向きが同じであれば、同じ過熱度ΔTに対応する熱流束qの値は液体水素が一番大きく、三重点液体水素とスラッシュ水素は同じ熱流束値との結果を得ている。本実験では同じ過熱度 ΔTに対し熱流束qの値は大気圧液体水素、三重点液体水素、スラッシュ水素の順で小さくなっており、三重点液体水素とスラッシュ水素の熱流束値の差は小さいが、明らかに差が認められる（後述の水素、窒素の 熱流束qvs. 熱伝達係数hの図参照）。

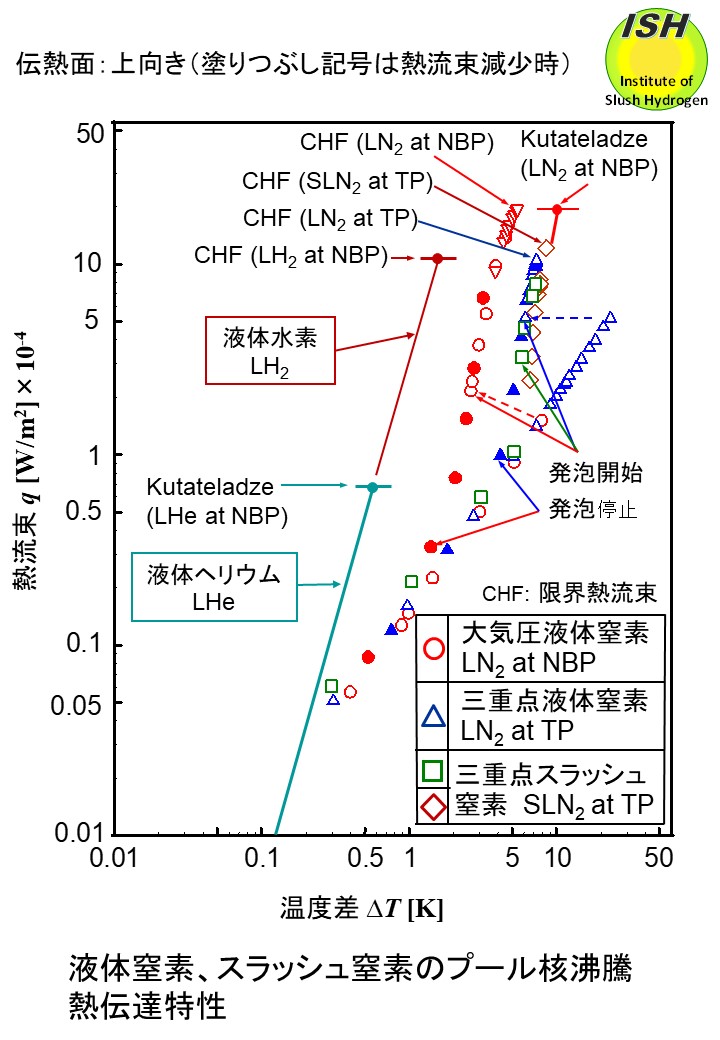
　因みに液体窒素の場合、下図に示すように限界熱流束　q*＝20 W/cm²（ΔT＝12 K）は液体水素より約 2倍大きいが、同一熱流束において熱伝達率は小さくなる欠点があり、液体水素の熱伝達率の方が優れている。

　伝熱面が上向きの場合の大気圧液体窒素、三重点液体窒素、三重点スラッシュ窒素の熱流束q、伝熱面との温度差（過熱度）ΔTを下図に示す。

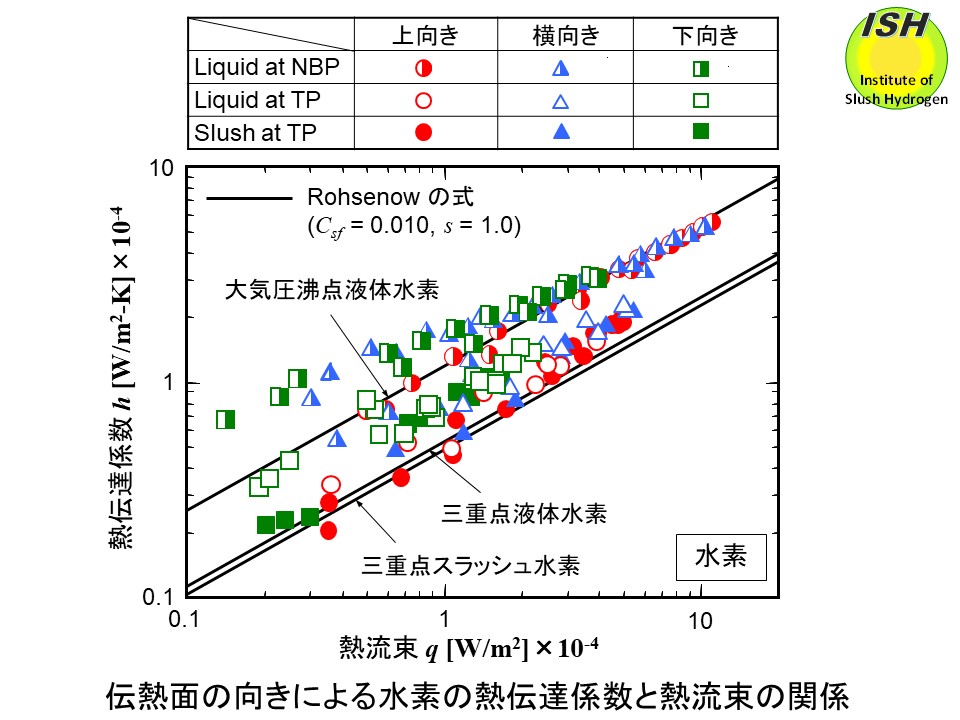
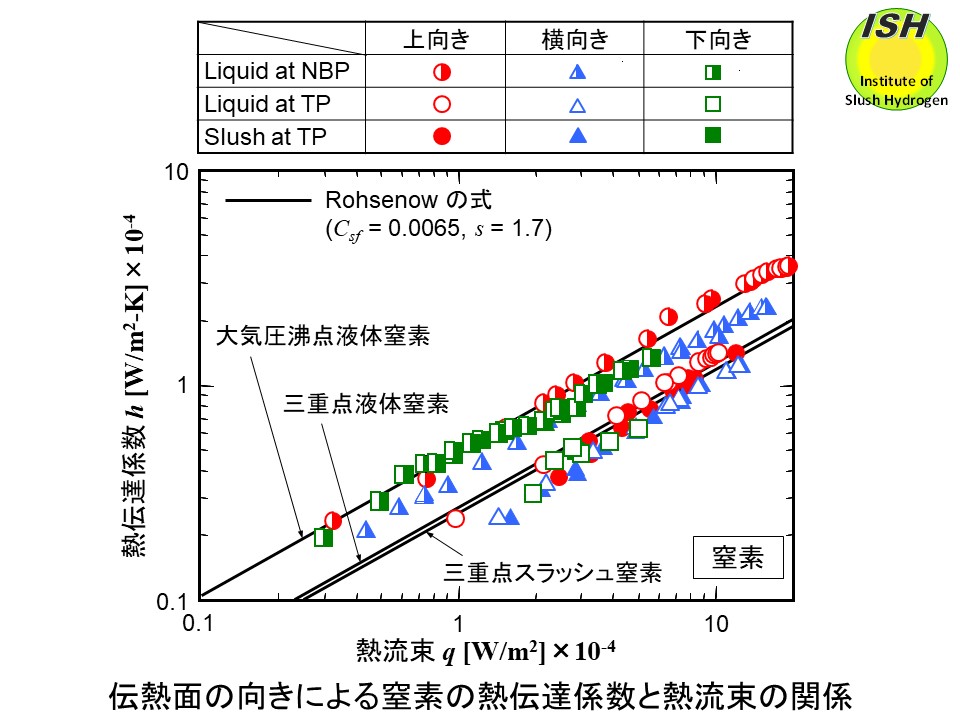
　水素および窒素について伝熱面の向きを変えて（上向き、横向き、下向き）、大気圧液体、三重点液体、 三重点スラッシュの核沸騰熱伝達率を測定した結果を下図に示す [28]。図中の実線は後述の Rohsenow 式により大気圧液体の実験結果から計算した結果である。

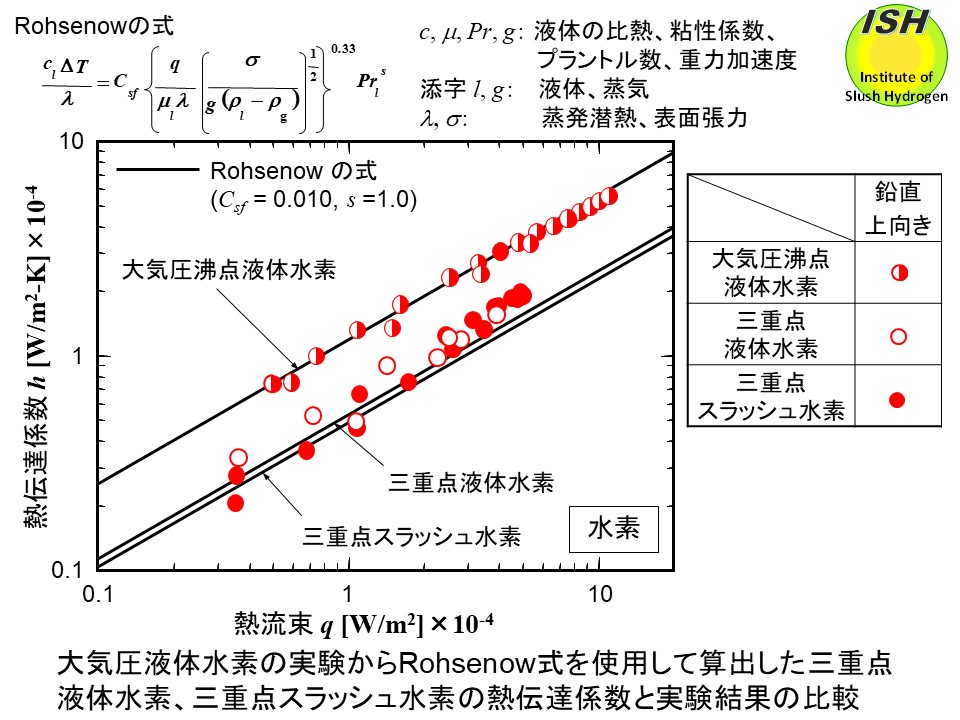
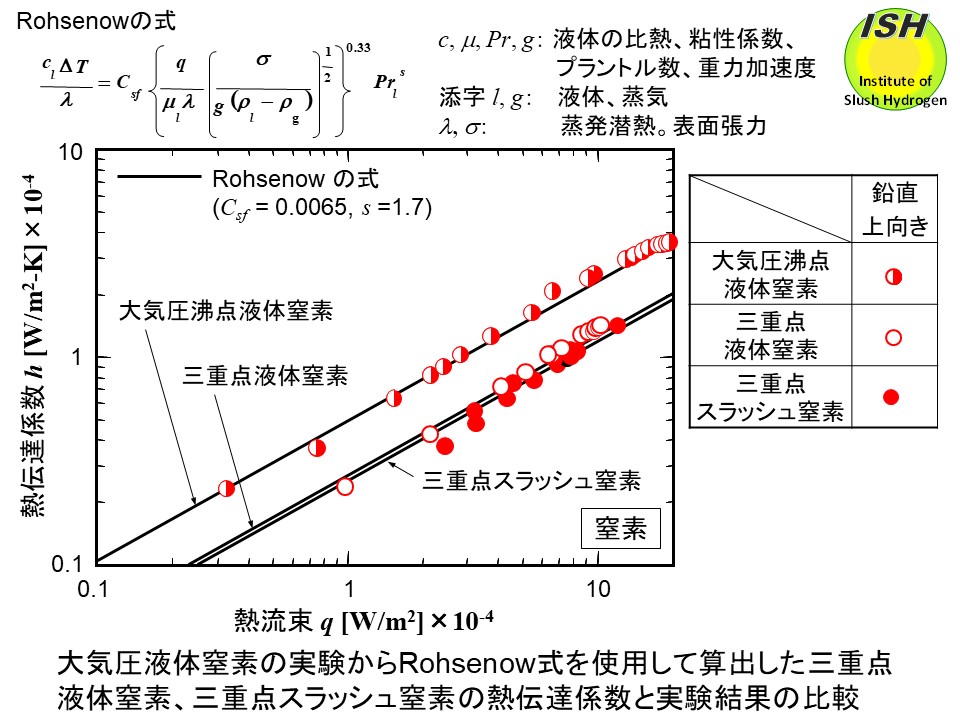
　Rohsenow は水などの室温単相液体の実験データから上向き伝熱面の核沸騰熱伝達率の式（下図）を提案している [34]。係数C_sfとsは伝熱面の材質と液体の組合せによって決まる値であり、圧力が異なる場合にも同じ値が適用できる。
　実験で得られたスラッシュ水素、スラッシュ窒素の結果を Rohsenow 式と比較し、固液二相流体への適用可能性を検討した。流体の物性値は大気圧沸点、三重点における値を用いた。まず、大気圧液体の実験結果を良く表すようにC_sfとsを決定した後（水素の場合、C_sf＝ 0.010、s＝1.0、窒素の場合、C_sf＝0.0065、s＝1.7）、三重点液体、スラッシュの熱伝達率を予測した。大気圧液体の実験結果を用いてスラッシュの熱伝達率が予測できることは実験の難しさを考えると実用上重要である。スラッシュの場合、蒸発潜熱λに固体の融解熱を含めた値を用いた。上向き伝熱面の計算結果を下図に実線で示す。大気圧液体水素、液体窒素の実験結果から Rohsenow 式を用いて三重点スラッシュ水素、スラッシュ窒素の熱伝達率を予測した結果、水素の場合、高熱流束域において実験結果よりやや低い値を予測するが、熱伝達率の予測は十分可能である。

　大気圧液体水素およびスラッシュ水素の限界熱流束値を液体ヘリウムの限界熱流束値と比較すると、高い限界熱流束値を持っており、高温超伝導材（MgB₂）を利用した高温超伝導機器の冷媒として液体水素もしくはスラッシュ水素の利用が充分に期待できる。

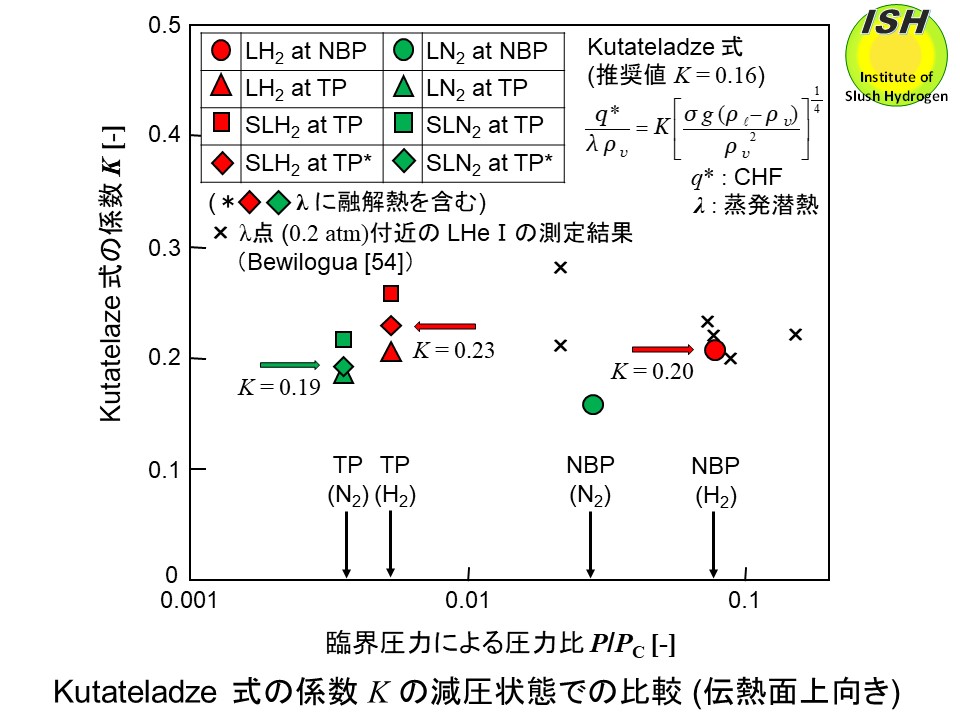
　Kutateladzeは水平伝熱面の核沸騰熱伝達における限界熱流束q*の式を下図に示す形で与えている [34]。伝熱の状況等によって係数Kの値は異なるが (0.095 ≤K≤ 0.20)、一般には Kutateladze が提案したK＝0.16 が実験値とよく合う平均的な値として推奨されている。
　大気圧液体、三重点液体、スラッシュの場合について、式の係数Kを上向き伝熱面の限界熱流束値から計算した結果を下図に示す。横軸には各々の流体の圧力と臨界圧力の比 (P/P_c) をとっている。スラッシュについては固体の融解潜熱を蒸発潜熱に含めて計算した値も示している。図には Bewilogua ら [54, 55] が液体ヘリウムのλ点 (P/P_c＝0.02)付近で測定した結果も示している。従来、P/P_c＝0.02 以下での測定例は無く、本実験結果では、水素、窒素いずれの場合も三重点液体、スラッシュの順に大気圧液体よりもKの値は増加の傾向を示しており、スラッシュの場合、K＝0.23 (H₂)、0.19 (N₂) 程度である。（固体の融解潜熱を蒸発潜熱に含めた時の値）

　伝熱面の傾きによる限界熱流束q*の変化を示したのが下図である。図には Kutateladze式の係数K＝0.16 として計算した限界熱流束q*の結果を上向き伝熱面の値として参考までに示した。スラッシュの場合は蒸発潜熱λに固体の融解潜熱を含めて計算した。また、図には上向き伝熱面を基準にして Vishnev [54] の関係式を示している。Vishnev 式では Kutateladze 式の係数Kの代わりに、K' ＝K(190-Φ)^0.5/190^0.5を使用している。
　Lyon [56] は臨界点からλ点までの液体ヘリウム中で実験を行い、伝熱面傾き角 (Φ) が増大するにつれて限界熱流束が減少する傾向を得ている。液体水素、液体窒素については、三重点圧力付近で伝熱面傾きによる限界熱流束の変化を系統的に実験した報告例は無いが、Class ら [57] が 0.82 atm の液体水素中で傾き角Φ＝0°、45°、90°で実施した例では、３種類の傾き角に対し、限界熱流束は殆ど差がない結果が得られている。本実験結果では、三重点液体およびスラッシュでは横向きの場合に上向きの場合より若干高い値を示している。また、Vishnev の関係式と比較すると横向き、下向きいずれも実験値の方が高い値を示している。スラッシュ水素、スラッシュ窒素の限界熱流束値は上向き伝熱面の場合、大気圧液体の 0.45倍、0.62倍に低下している。下向き伝熱面の場合、それぞれ上向きスラッシュの 0.33倍、0.43倍に低下している。