水素の凝縮熱伝達率が Nusselt理論式と一致することを世界で初めて実証

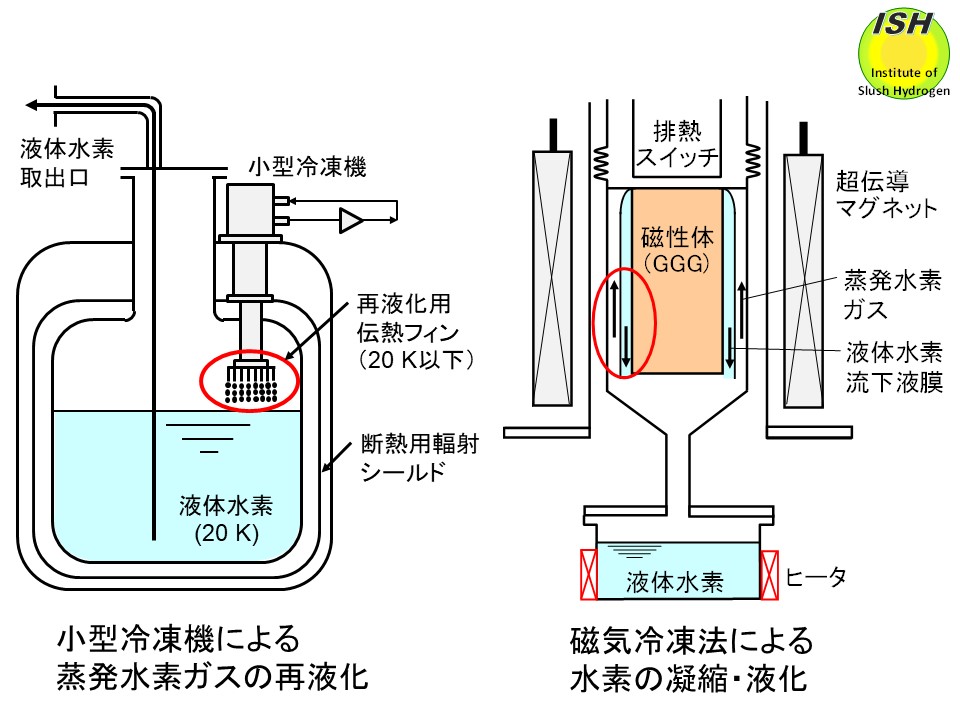
　燃料電池の燃料を液体水素の形態で輸送・貯蔵する場合、輸送時や消費地に設置された液体水素貯槽から発生する蒸発ガスの再液化が経済性の面から重要となる（上図の小型冷凍機による蒸発水素ガスの再液化）。凝縮・液化時の熱伝達率を精度良く推定することは熱交換器（凝縮器）の設計上重要となるばかりでなく、液化に要する所要動力も低減できる。

　ここでは、"世界初の磁気冷凍法による高効率水素液化技術の開発"に際し、必要となった水素の凝縮・液化技術（上図の磁気冷凍法による水素の凝縮・液化）について紹介する。

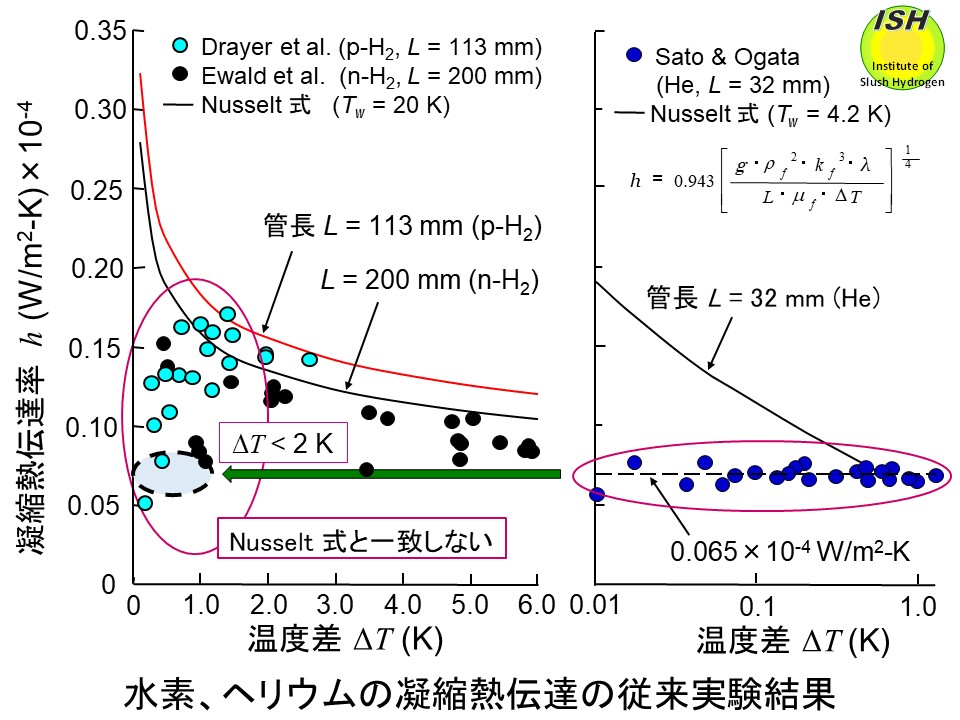
　鉛直管内もしくは管外で流体が膜状凝縮する際の熱伝達特性に関する研究は、上図に示す Nusseltの鉛直平板上での層流膜状凝縮理論に始まる。極低温流体*の凝縮・液化の研究は少なく、液膜が層流の場合については数例実施されているのみである。酸素、窒素など比較的沸点の高い極低温流体については、凝縮・液化時の熱伝達率が Nusselt層流理論式と良く一致することが確認されている。これに対し、下図の水素、ヘリウムに示すように、沸点の低い水素、重水素、ヘリウムは Nusselt理論式と一致しない実験結果が従来得られていた（Lは管長） [34]。

　特に凝縮器の設計に重要となる凝縮ガスと伝熱面の温度差 ΔT（過冷度）が小さい場合（ΔT＜ 2 K）、理論式との差が大きくなる傾向を示しており、実験から得られた凝縮熱伝達率　hと Nusselt理論式との関係は長い間、明確にされていなかった。その原因としては、極低温下での実験方法、実験装置、実験精度の問題があげられる。

　超伝導マグネットを使用した医療用MRI装置では、蒸発したヘリウムガスを小型冷凍機で凝縮・液化する方式が一部採用されているが（上図の小型冷凍機による蒸発ガスの再液化）、温度差 ΔTが小さい場合の熱伝達率は定量的に明確にされず使用されている。

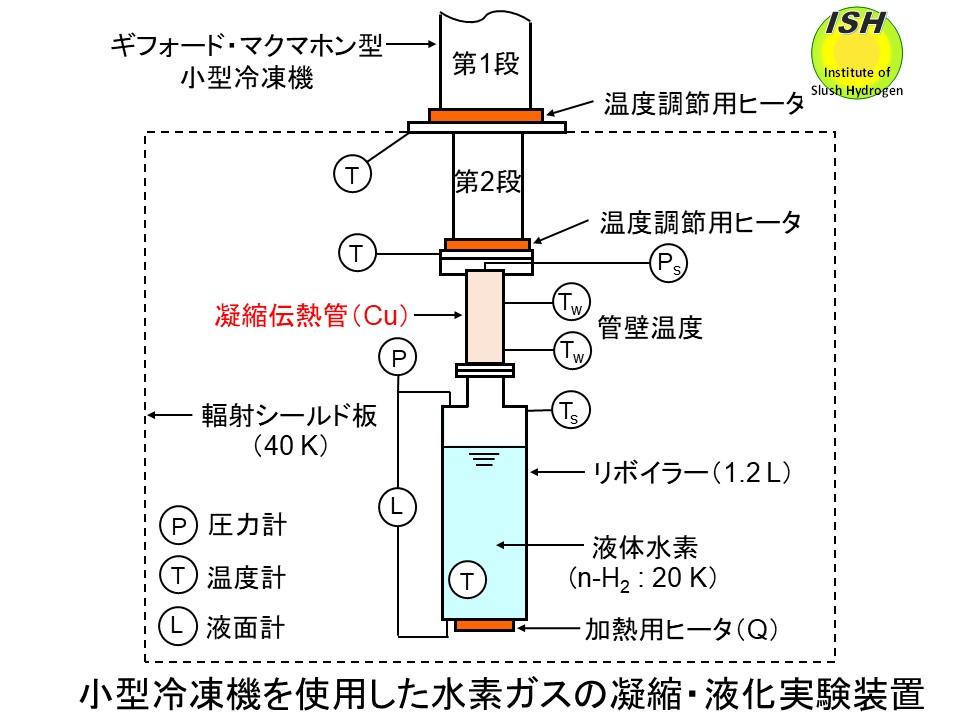
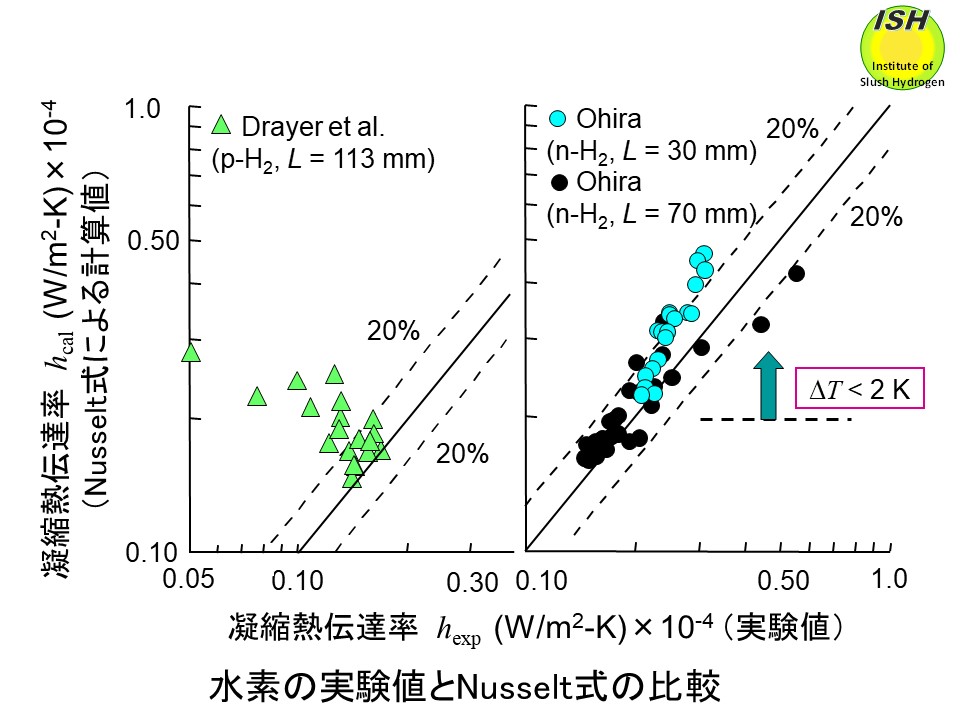
　液体水素容器内で蒸発する水素ガスが凝縮・液化する際の凝縮熱伝達率　hを、下図に示すG-M型小型冷凍機（三菱重工製 UCR31W）を使用した実験装置で測定した。本実験装置は、貯槽から蒸発する水素ガスの再液化（上図）をシミュレートするものである。下図に示す実験結果から、水素の熱伝達率は Nusselt 層流理論式と±20%程度で良く一致することを世界で初めて実証した [7]。実験で得られた水素の凝縮数　Nu*と膜レイノルズ数　Re*の関係を下図に示す。また、従来報告されている酸素、窒素、水素、ヘリウムの実験データも併せて示す。Nusselt理論式から導かれる凝縮数と膜レイノルズ数の関係式を比較のために実線で示している。

　本実験で得られた結果は、重水素、ヘリウムの場合でも凝縮液膜が層流の場合、凝縮熱伝達率は Nusselt 層流理論式から予測できることを示唆しており、工学上非常に有用である。例えば、液体水素貯槽で侵入熱により蒸発する水素ガス（ボイルオフガス）や医療用MRI装置の液体ヘリウム貯槽で蒸発するヘリウムガスを高効率で再液化できる。また、磁気冷凍法により温度 -259℃（絶対温度 14 K）以下の寒冷を発生させると、液体水素からスラッシュ水素の製造が可能となる。

　* 極低温流体：大気圧沸点の温度が -150℃以下の流体。メタン、酸素、窒素、ネオン、水素、ヘリウムなどがある。

従来実験結果と水素実験で得られた結果の比較