スラッシュ流体の圧力損失低減、熱伝達劣化、固体粒子挙動の数値解析(SLUSH-3D)
スラッシュ水素をパイプライン輸送する場合、移送管、バルブ、収縮・拡大管、エルボ等の圧力損失が輸送効率を向上する上で重要となる。また、パイプラインでは極低温時の配管収縮を吸収するコルゲート管が多用され、その圧力損失も重要となる。スラッシュ水素輸送時の圧力損失増加はポンプ動力を増大させ輸送システムの性能を低下させる。
また、スラッシュ水素を高温超伝導送電の冷媒として利用する場合、超伝導線のクエンチ等による発熱が想定され、伝熱時の圧力損失と強制対流熱伝達の両者がパイプライン設計上重要である。
スラッシュ窒素の圧力損失低減、伝熱劣化の実験結果
スラッシュ窒素(温度 63 K)を使用して水平管内流動、伝熱特性の実験を行い、液体窒素と比較した圧力損失低減、熱伝達率劣化が同時に発生することを世界で初めて実証し、低減、劣化メカニズムを解明した。即ち、同じ流動条件では、圧力損失(流体摩擦係数)が減少すると熱伝達(熱伝達係数)も同時に減少する「レイノルズのアナロジー」(Reynolds' analogy)が固液二相流体であるスラッシュ流体でも成立することを我々は初めて実証した。 (下記Web site: スラッシュ窒素の圧力損失低減と伝熱劣化 参照)
水平円管を流動する際、高流速時に固体粒子が管内に一様に分布する擬均質流において、液体窒素よりも圧力損失が小さくなる圧力損失低減が現れる [16,
17]。内径 10 mm、15 mm の場合、流速 2.0 m/s 以上、3.6 m/s 以上で液体窒素(63 K)よりも圧力損失が各々最大
25%、23% 低減する。加熱時(熱流束 10 kW/m2)でも圧力損失が最大 23%、17% 低減し、熱伝達率も液体窒素よりも最大 27%、20% 劣化する [18, 19]。
一辺 12 mm の水平正方形管では流速 2.5 m/s 以上で圧力損失が最大 12% 低減し、熱流束 10 kW/m2でも圧力損失が最大 12% 低減し、熱伝達率も最大 16% 劣化する [20]。
正三角形管(一辺 20 mm、水力直径 D=11.55 mm)では、 頂点が上向き、横向き、下向き(逆正三角形)の3種類の断面姿勢で実験を行った結果、流速 1.3-1.8 m/s 以上において圧力損失低減が現れ、最大低減量は加熱の有無によらず
16-19%であった。熱伝達劣化は 1.2-1.8 m/s 以上の流速で現れ、最大劣化量は 13-16%であった [5, 21]。
熱流束 0 kW/m2において内径 15 mm の収縮・拡大管では流速 1.5 m/s 以上で圧力損失が最大 50% 低減する。また、内径 12 mm、15 mm
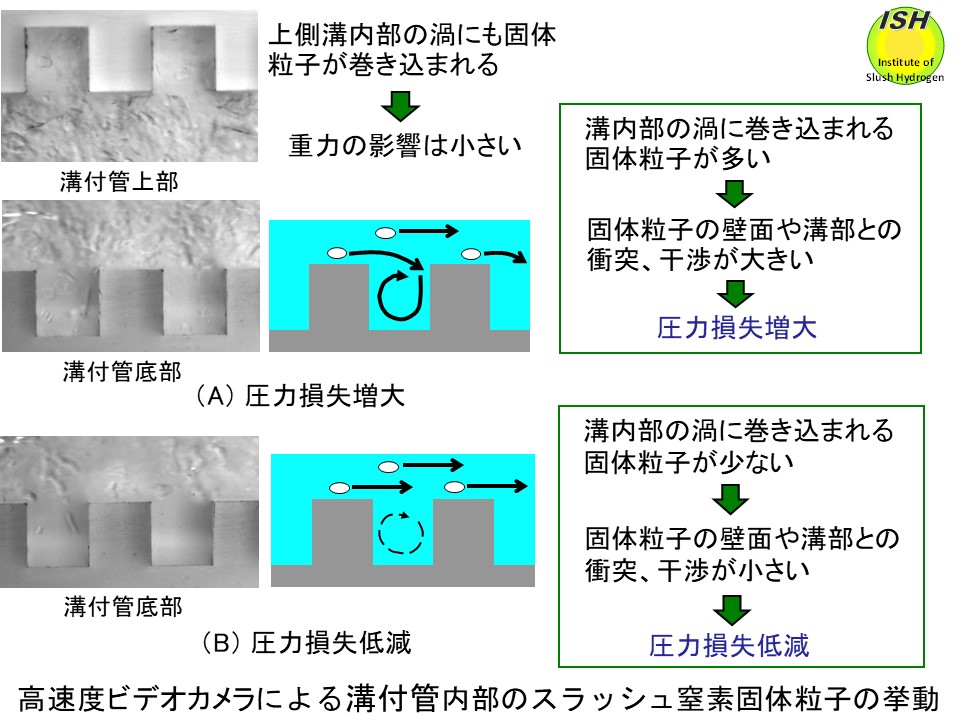
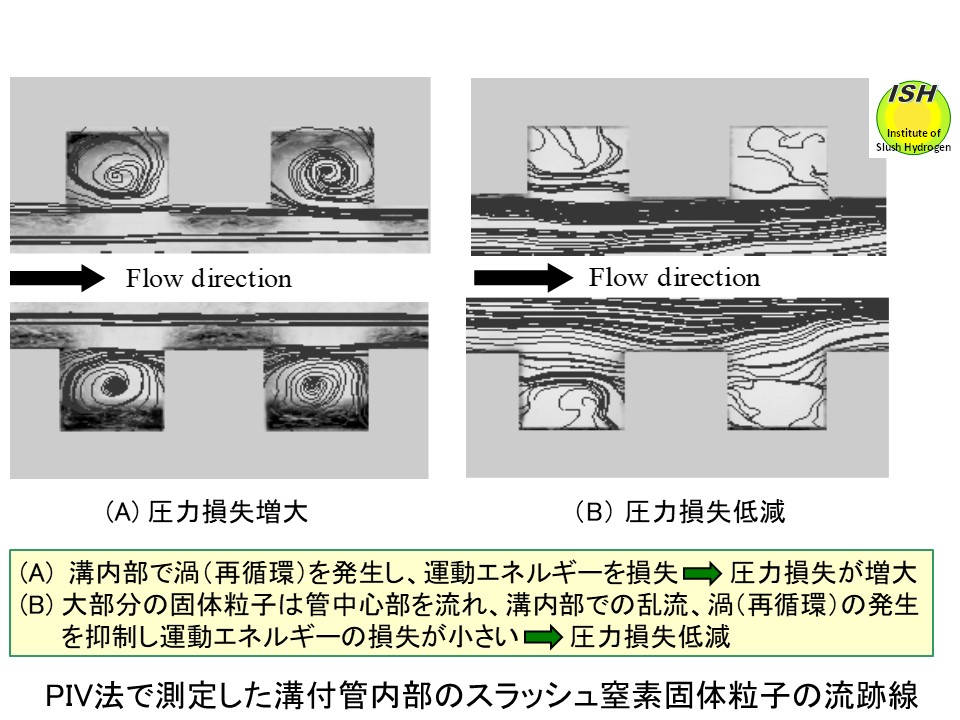
の2種類のコルゲート管では流速 2.0 m/s 以上において圧力損失が各々最大 37%、31% 低減する [22, 23]。圧力損失低減メカニズム解明のため、コルゲート管を模擬した溝付管内のスラッシュ窒素固体粒子の流動を高速度ビデオカメラで可視化観察した結果と流跡線をPIV法*で測定した結果を各々下図「スラッシュ窒素の流動特性、圧力損失低減 と伝熱劣化特性」に示す。擬均質流となる高流速時においては、大部分の固体粒子が管中央部に移動し管壁、溝内部の乱流、渦(再循環)の発達を抑制し圧力損失低減が発生する。
内径 15 mm のエルボでは流速 2.0 m/s で最大 10%の圧力損失低減が発生する [24]。
加熱時、非加熱時共に、摺動流から擬均質流に変化する高流速時には、管中央部に移動した固体粒子群によって管壁での乱流発達が抑制され、圧力損失低減が発生する**。一方、熱伝達は管壁付近の固体粒子の少ない液体層で行われるが管壁での乱流発達が抑制されるので管壁付近の加熱された液体が管中央部へ拡散する作用も抑制され、熱伝達劣化が発生する**。スラッシュ流体は配管内流動時に圧力損失低減の大きなメリット(ポンプ動力低減)があるが、熱伝達劣化のデメリットもある。然しながら、固体粒子径を調整することにより、圧力損失低減量をある程度保持しつつ熱伝達劣化量を小さく保持することが可能であり、用途に応じてスラッシュ流体のメリットを十分に生かすことができる。固体粒子径の調整には「スラッシュ水素、スラッシュ窒素製造」のページで述べた「オーガ法」を使用する。
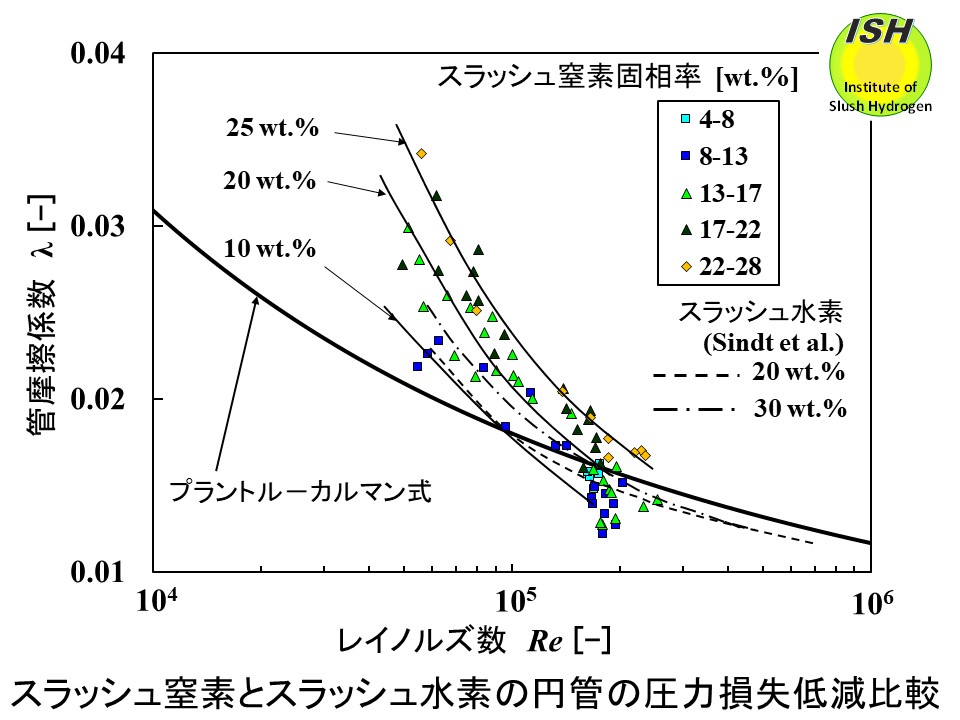
スラッシュ水素の実験データは水平円管(内径 16.6 mm)を流動する Sindt らの結果が1例のみ報告されている [29]。スラッシュ窒素で得た実験結果(内径
15 mm)と共に管摩擦係数λとRe数(レイノルズ数)の関係を上図に示す。液体単相のプラントル-カルマン式も示す。
スラッシュ水素、スラッシュ窒素いずれもRe数が 1.0×105以上で圧力損失低減が現れ、固相率が増大すると低減開始Re数は大きくなる。同程度の固相率(20 wt.%)で比較すると低減開始のRe数はスラッシュ水素の方が小さい。スラッシュ水素とスラッシュ窒素の動粘性係数は同程度であり管内径も同程度であることから、スラッシュ水素はより低流速で低減が現れることを示している。液体水素と液体窒素の密度比、粘性係数比はいずれも
1/11、スラッシュ水素の固液密度比は 1.12(スラッシュ窒素 1.18)と小さいことから、スラッシュ水素はより低流速で擬均質流となり、圧力損失低減が現れることになる。
スラッシュ流体が管内を流動する際の流動・伝熱現象は固体粒子の挙動と相俟って非常に複雑である。実験および数値解析の両面から精度良く現象解明を行うことを目的として三次元流動・伝熱解析プログラム(SLUSH-3D)を独自に開発した [25, 26]。本解析プログラムは物性値を考慮することにより、スラッシュ水素、スラッシュ窒素のいずれにも適用可能である。
スラッシュ窒素の圧力損失低減を数値解析で再現したとする論文 ➡ 結論:科学的根拠が無い前代未聞の酷い論文である
固体粒子と液体の固液二相管内流動現象は三次元であり、二次元数値解析では解明できないのであるが、スラッシュ窒素の水平直管内三次元流動を水平な平行平板内二次元流動と見做して二次元数値解析を実施した結果、「直管内を流動するスラッシュ窒素の圧力損失が液体窒素よりも低下することを数値解析により再現した」との論文がある。この論文には科学的根拠が全く無いことを以下に示す。
直管内流れと平行平板内流れでは流動現象が全く異なるので平行平板内の二次元数値解析結果は直管内の三次元流動には適用できない。大容量、高速のコンピュータが普及している現在、三次元流動解析ができる計算を二次元解析するのは「時代錯誤」(時代遅れ)も甚だしい。後述のように二次元数値解析で得られた流動現象、管摩擦係数が実際とは異なることに何ら疑いを持たず、一般に良く知られている実験結果との比較、検証さえも行っていない。科学的根拠の無いスラッシュ窒素と液体窒素の計算結果のみを相互比較して圧力損失低減を再現したと結論している。これらの点からも数値解析、流体工学に関する基礎知識(常識)、研究能力が欠如していることが判る。
液体窒素(単相)の平行平板内流れの二次元数値解析結果をアスペクト比の異なる2種類の三次元直管内流れに適用して、各々のアスペクト比に対応して2種類の管摩擦係数曲線を論文に示している。アスペクト比(AR)を
AR=(管長L)/(管径D) で定義し、2種類の AR= 7.5、15 で解析しているが、ARが小さいため流路後半部が定常流となっていない。管摩擦係数は定常流の圧力損失から算出される値であり、多くの単相流の実験データを集大成した有名なニクラゼ(Nikuradse)式(もしくは上図のプラントル-カルマン式)の曲線で示されるように、レイノルズ数から一意に決定されるのが流体工学の「常識」(定義)であり、定常流ではアスペクト比により管摩擦係数が異なることは絶対にあり得ない。レイノルズ数は流体の密度、粘性係数、管内流速、管径Dからなる無次元数であり、管摩擦係数は管長Lもしくは AR には関係しない。論文に掲載されているスラッシュ窒素と液体窒素の管摩擦係数の計算結果に、ニクラゼ式から算出される液体窒素の管摩擦係数を我々が別途付け加えた図を下図に示す。レイノルズ数Re=4×105での液体窒素の管摩擦係数はニクラゼ式(実験値)の 0.0136 に対し、論文では AR=7.5 の場合 0.044、AR=15 の場合 0.124
であり、数値解析結果はニクラゼ式とは大きく(数倍)異なっているのが一目瞭然である。スラッシュ窒素の場合でも同様に2種類の管摩擦係数曲線を算出している。即ち、レイノルズ数Re=7×104での管摩擦係数は我々のスラッシュ窒素実験結果(固相率20%)が 0.025 程度に対し、同一固相率20%において論文では AR=7.5 の場合
0.072、AR=15 の場合 0.084 であり、液体窒素の場合と同様、数値解析結果は我々の実験値と大きくかけ離れている。
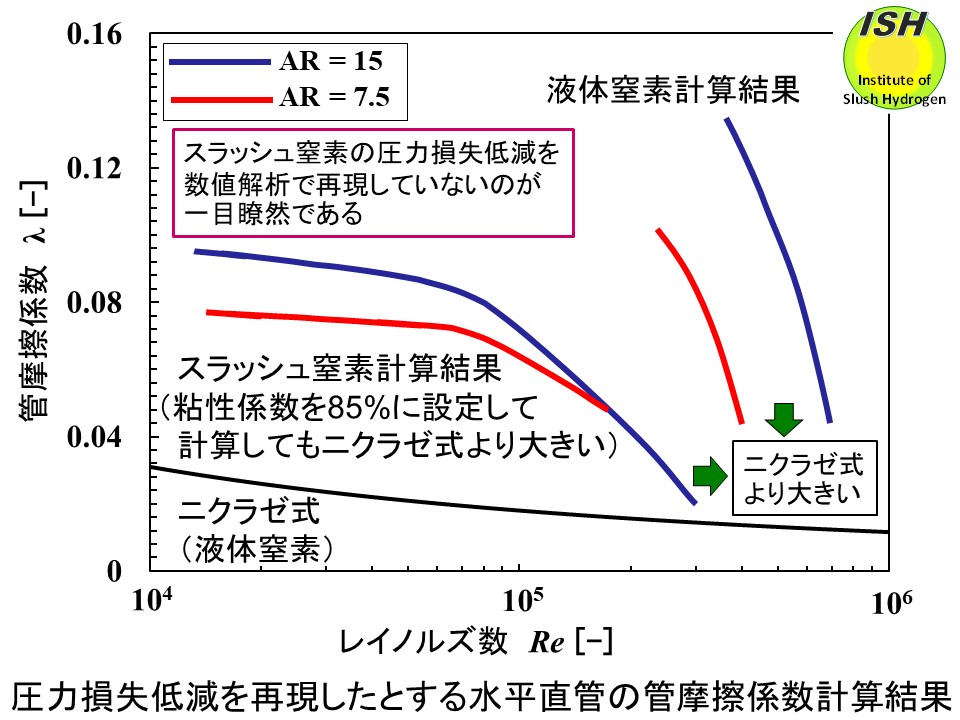
実際の流動では流路入口で入口効果により圧力損失が急激に増大し、その後、下流で定常流になるに従って流動が整定し圧力損失は小さくなり一定の圧力損失となる。この一定の圧力損失から管摩擦係数を算出する。論文では圧力損失の解析結果が流路後半部で一定値に収束する(定常流になる)傾向があるにも拘わらず、管摩擦係数がニクラゼ式(液体窒素)、スラッシュ窒素実験値の数倍となることは絶対にあり得ない。上図の解析結果から、同一レイノルズ数でスラッシュ窒素の圧力損失が液体窒素よりも小さくなっているのはスラッシュ窒素中の固体粒子と液体窒素の運動量交換による圧力回復が原因であると素人考えの尤もらしい出鱈目を科学的根拠も示さずに述べている**。直管上流では運動量交換が行われる非定常流であるが、下流では運動量交換が終了して管摩擦係数(圧力損失)が一定となる定常流となる。この一定の管摩擦係数と液体窒素単相流の定常流での管摩擦係数を比較して圧力損失低減が発生していると断定できる。管摩擦係数は定常流での値であり、流動時の運動量交換メカニズム、および非定常流と定常流の違いを理解していない出鱈目な解析結果には科学的根拠は無い。スラッシュ窒素の圧力損失が小さくなっているのは、後述のようにスラッシュ窒素中の液体窒素の粘性係数を実際の物性値よりも小さく設定し(物性値の85%)、液体窒素単相流の解析では実際の物性値を粘性係数として設定しているのが原因である。液体窒素とスラッシュ窒素の解析結果が正しいと信じ込んでおり、両者を比較した結果から圧力損失低減が得られたと考えている。解析結果が間違えていることはニクラゼ式、他文献のスラッシュ窒素実験値と比較すれば一目瞭然である。粘性係数を小さくして計算すれば圧力損失が小さくなるのは当然であり直管の圧力損失低減メカニズム**を理解していない。この論文の筆頭著者が流体工学、数値解析の「素人」であり、解析手法、解析プログラム、数値解析結果が全くの出鱈目であることが最大の問題点である。
我々はスラッシュ窒素が収縮・拡大管(直管ではない)を流動する際に現れる圧力損失低減が固体粒子と液体窒素の運動量交換による液体窒素の圧力回復であること(低減メカニズム)を科学的根拠(PIV流速測定)を示して既に解明している(下記Web
site の収縮・拡大管内流動、圧力損失低減、PIV流速測定のページ参照)。
ARが小さいため、論文では流路下流で定常流を再現できず中途半端な解析結果を「非定常二相流」と称し、管摩擦係数の算出を行っている。実際の非定常二相流動現象ではなく、数値解析の収束過程であることを理解していない。さらに「非定常二相流」と称する解析結果では、液体窒素の粘性係数を実際の物性値よりも小さく設定していること、後述のように、液体窒素の流速分布が流体工学、数値解析の「基礎知識(常識)」である壁面でのノンスリップ条件(壁面での流速ゼロ)を満足していないことから、実際の流動をシミュレートしていないことは明らかである。この出鱈目な解析結果を基に算出した管摩擦係数の数値は科学的根拠が全く無い。
管摩擦係数を算出した直管流路の位置(入口からの下流位置)を記載するのが流体工学の「常識」であるが、論文には記載がない。ARが小さいので流路の一部でさえも定常流となることはなく「非定常二相流」と称して数値解析結果を基に管摩擦係数を算出している。その結果、液体窒素、スラッシュ窒素の各々について流体工学では何ら意味の無い2種類(各々
AR=7.5、15 の合計4種類)の管摩擦係数(縦軸)とレイノルズ数(横軸)の曲線を得ている(上図)。数値解析で得た液体窒素の管摩擦係数曲線の図とニクラゼ式(液体窒素)の管摩擦係数曲線の図(他文献からの単なる引用図)を論文の同一ページに並べて掲載しているにも拘わらず、両者の管摩擦係数の値、曲線形状が異なること(例えば、解析結果が上に凸、ニクラゼ式が下に凸の曲線形状、上図)、レイノルズ数が大きくなると(105オーダ)「数値解析で得た管摩擦係数がゼロ以下の負の値」となることには何ら疑問を持たず、数値解析結果は正しいと信じ込んでいる。この論文の筆頭著者は、流体工学の「常識」である① 流体の直管内流動では流路入口から所定の助走区間(非定常流)を経て定常流に遷移する ② 管摩擦係数は定常流の圧力損失から算出する値であることさえも理解していない。
論文では「数値解析で得たスラッシュ窒素と液体窒素の管摩擦係数を高レイノルズ数領域で比較した結果、スラッシュ窒素の管摩擦係数が小さいので、圧力損失低減を数値解析により確認した」と結論付けている。これまで述べたように数値解析(二次元)が実際の流動(三次元)をシミュレートしておらず、定常流の数値解析結果さえも得られていないので(ARが小さ過ぎる)両者の管摩擦係数は出鱈目であり、出鱈目な結果を比較した結論には科学的根拠は無い。得られたスラッシュ窒素の管摩擦係数が信憑性のある値と仮定しても、全てのレイノルズ数でニクラゼ式(液体窒素)よりもはるかに大きい値であり、数値解析による圧力損失低減を再現していないのは明らかである。管摩擦係数を議論する論文であるのに、上図に示すように論文中で数値解析結果とニクラゼ式(実験値)の比較を一切行っていないのは、流体工学で有名なニクラゼ式の存在と式の意味さえも知らない初歩的な知識不足(流体工学の研究者として致命的)によるものである。
流体工学および数値解析に関する初歩的(致命的)な知識不足をさらに指摘すると、平行平板内のスラッシュ窒素流動解析では管摩擦係数(圧力損失)を小さく算出するためにスラッシュ窒素中の液体窒素の粘性係数を実際の物性値よりも小さい値(物性値の85%)に設定している(実際の低減量20%程度に対応して設定)。粘性係数を小さくすれば圧力損失低減が出現する解析結果が当然得られるはずであるが、得られたスラッシュ窒素の管摩擦係数をニクラゼ式(液体窒素)と比較しておらず、圧力損失が実際の液体窒素よりも低減していないこと(上図)にも気付いていない。即ち、数値解析方法、解析プログラムが根本的に間違っていることを認識していない。粘性係数を物性値より小さく(85%)設定する解析行為は低減現象の本質を理解しておらず、邪道であり、研究者倫理に背く恥ずべき行為である。
また、開発したとする二次元数値解析プログラムで得た流速等の計算結果と実験データとの事前検証結果が示されておらず数値解析結果の精度が不明である。数値解析で「常識」となっている事前検証(例えば、上図のように液体窒素の管摩擦係数計算結果とニクラゼ式との比較)を行えば、開発したプログラムが実際の流動現象をシミュレートしていないことは一目瞭然である。スラッシュ窒素の数値解析で同時に得られる液体窒素の流速分布においても壁面でのノンスリップ条件(壁面での流速ゼロ)さえも満足しておらず、通常の流れ(管径方向に放物線状の流速分布)とは異なる流速分布となっている。流路入口で放物線状の流速分布を「境界条件」と称して与えているが、流路内での流速分布を計算するのが目的であるので「境界条件」ではなく「初期条件」であり、流路壁面での「境界条件」であるノンスリップ条件を与えていないため管径方向に放物線状とは異なる流速分布となっている。数値解析の常識である「初期条件」、「境界条件」の定義、設定方法さえも理解していない。さらに、水平狭まり-広がり管(収縮・拡大管)内のスラッシュ窒素の流動についても水平直管と同じ手法で解析しており、実際の流動現象とは異なる間違った解析結果(壁面での液体窒素の流速がゼロでない、スロート部直下流での流速分布が実際とは異なる等)を得ているのが一目瞭然である。数値解析、流体工学に関する基礎知識(常識)、研究能力が欠如している。
因みに、我々が開発したSLUSH-3Dの解析では円管径D=15 mm の場合、管長L=600 mm として(論文での AR=40)、プログラムの事前検証(PIVでの管内流速測定結果、プラントル-カルマン式との比較)を行った後、圧力損失が一定値に収束する流路入口から
400 mm での計算結果を採用している。また、流路出口部の上流への影響を極力小さくするため出口から上流 200 mm としている [25]。前述のように、我々は可視化実験を含めた実験および数値解析で得た固体粒子と液体窒素の複雑な流動現象を基に圧力損失低減メカニズム**を既に解明しており
[5, 16-19, 25, 26]、得られた低減メカニズムをモデル化し、圧力損失低減を数値解析で再現する研究をこれまで実施してきた(当然であるが、液体窒素の粘性係数は物性値をそのまま使用して計算する)。現状、数値解析で圧力損失低減を再現するまでには至っておらず、他の研究者からも再現したとの報告はない。
以上により、数値解析方法(解析プログラム)、解析結果も含め、水平直管内流れにおけるスラッシュ窒素の圧力損失低減を数値解析で再現したとする論文(国内学会誌、英文ジャーナルに掲載中)には科学的根拠が全く無い。この論文に科学的根拠が無いことを理解できずに参考文献として引用している論文がある。流体工学、数値解析、スラッシュ流体に造詣の深い研究者は自身の学術価値の高い論文では、この科学的根拠が全く無い、前代未聞の酷い論文 を参考文献として引用しない。自身の論文の学術的価値が損なわれるためである。
この論文の筆頭著者は「スラッシュ水素、スラッシュ窒素製造」のページで述べた「エジェクタ法(二流体ノズル)によるスラッシュ窒素製造に関する数値解析」の論文著者である。エジェクタ法では液体ヘリウムを使用しており、① エジェクタ効果は効率が非常に悪い ②液体ヘリウム使い捨てであるため、稀少なヘリウム資源の枯渇問題がある ③ 製造したスラッシュ窒素中にはヘリウムが溶解しており、僅かな圧力、温度変動によりヘリウムの気泡が発生し伝熱性能が低下するので高温超伝導機器の冷媒として使用されない。高温超伝導機器に液体ヘリウム使い捨てのエジェクタ法を使用することは高温超伝導技術の普及に逆行しており、「高温超伝導システムの一部として機能しない」ことを論文著者は全く理解していない。即ち、エジェクタ法が高温超伝導機器の冷媒製造を目的としながら、「液体ヘリウムを使用し、使い捨てにする矛盾」に全く気付いていない 酷い論文である。エジェクタ法はスラッシュ窒素製造法として「最悪」であり、実用性は無い(誰も使用しない)。エジェクタ法の数値解析結果についても、これまで述べたように数値解析、流体工学に関する基礎知識(常識)、研究能力が欠如しており、学生のコンピュータ演習と同様、単に計算を実行したのみであり、この論文でも数値解析の「常識」である解析手法および計算精度の事前検証、解析結果と実験結果の比較検討さえも行っていない。数値解析結果に信憑性、科学的根拠は無い。実用性が無く、学術的価値も無いエジェクタ法の数値解析自体が本来無意味である。(当該ページを是非一読下さい)
SLUSH-3D を使用したスラッシュ窒素の流動、伝熱数値解析結果と実験結果(詳細は下記 Web site)
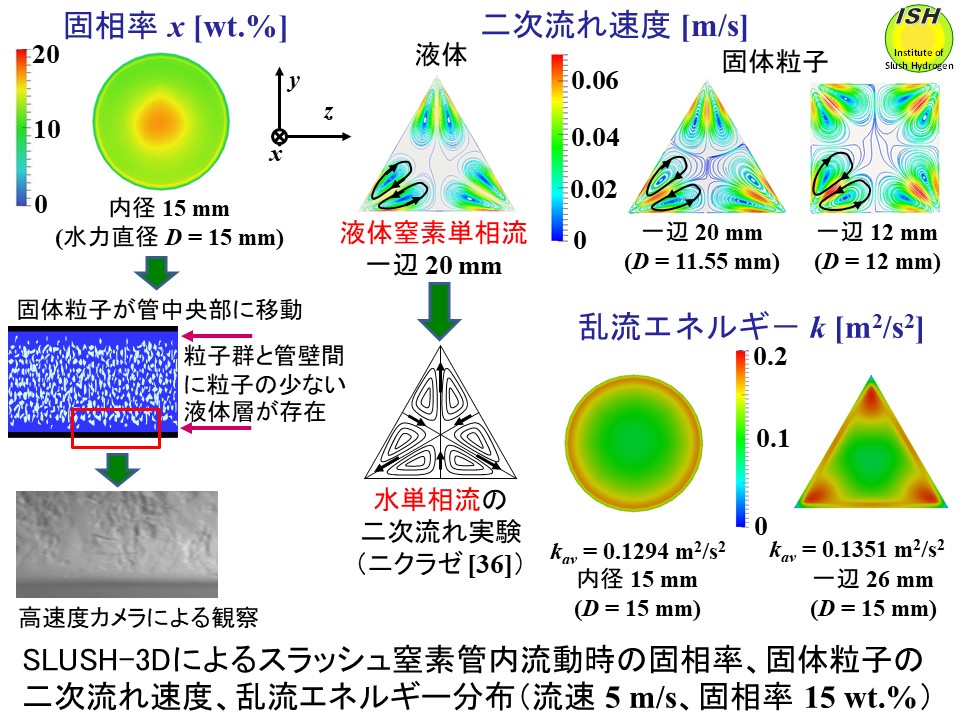
開発した三次元流動・伝熱解析プログラム(SLUSH-3D)を使用して[5, 25-27]、スラッシュ窒素が熱流束 0 kW/m2において、内径 15 mm の円管、一辺 20 mm、26 mm(水力直径D=11.55 mm、15 mm)の三角形管、一辺 12 mm(水力直径D=12 mm)の正方形管を流動する際の管断面での固相率分布、固体窒素粒子の第二種二次流れ速度分布(円管では出現しない)、液体窒素が保有する乱流エネルギー分布を解析した結果を下図に示す[5]。SLUSH-3Dでは非線形渦粘性(non-lineark-ε)モデルを使用して液体窒素、固体窒素粒子の三角形管および正方形管内の第二種二次流れを再現している。非加熱時において液体窒素単相流の第二種二次流れの数値解析結果はニクラゼ(Nikuradse)による有名な水の実験結果 [36]と良く一致することを事前に検証している(下図)。
下図左は固体窒素粒子間,および固体窒素粒子と壁面間の衝突を考慮した円管内の固相率分布の解析結果であり、擬均質流になると固体窒素粒子が管中央部に移動する現象を良く示している。下図右上の固体窒素粒子の第二種二次流れは、液体窒素と同様に管の中央部では殆ど存在せず、中央部から頂点へ流れる同じ大きさの渦を1つの頂点につき2個形成し、頂点から管壁に沿って流れた後、中央部に戻る。下図右下の乱流エネルギーkは x、y、z方向の乱れ速度の自乗和であり、kavは管断面での平均値である。
これまで、主に円管の圧力損失低減について述べてきた。水素貯蔵システムにおいては輸送用配管や超伝導送電用冷媒配管以外に熱交換器等でもスラッシュ水素の使用が予想され、スラッシュ流体が種々の断面形状をもつ配管内を流動する際の流動、伝熱特性が重要となる。極低温機器に多用されているプレートフィン型コンパクト熱交換器の流路は三角形もしくは矩形等であり、熱交換器の設置姿勢により流路が上向き、
横向き、下向き(逆三角形)となることが予想される。また、一般に三角形管は同一水力直径 (D) の円管、正方形管と比較すると伝熱面積(周長)が増加すると共に集積性にも優れる特徴がある。
熱流束 10 kW/m2において円管(内径 10 mm)、正方形管(一辺 12 mm)、上向き正三角形管(一辺 20 mm)の実験から得られた同一流速における圧力損失比 rdpと熱伝達率比 rhの相関関係を下図に示す [5, 6]。rdp、rhは液体窒素の圧力損失、熱伝達率を基準にしたスラッシュ窒素の圧力損失比、熱伝達率比である。3種類の管の水力直径は同程度である。
円管の最大低減量、最大劣化量は前述のように三角形管より大きいが、三角形管の rhは、円管、正方形管と比べると rdpよりも大きい傾向を示す(rh > rdp)。理由として次のことが考えられる。円管(内径 15 mm)、同じ水力直径をもつ三角形管(一辺 26 mm、D=15 mm)の乱流エネルギー分布を前掲右下図に示した。水力直径が同じ場合、頂点で発生する乱流エネルギーの影響により三角形管の方が円管よりも平均乱流エネルギーが大きくなる。従って、三角形管(一辺
20 mm、D=11.55 mm)と内径 10 mm 円管の比較においても三角形管の平均乱流エネルギーが大きく、三角形管の圧力損失低減効果、熱伝達劣化が乱流エネルギーにより抑制され、円管の方が圧力損失比と熱伝達率比が共に小さくなる(低減、劣化効果大)。
さらに、三角形管の場合でも円管と同様に大部分の固体粒子は前掲右下図に示す乱流エネルギーが小さい管中央部を流動するので3つの頂点付近には固体粒子の少ない液体層が円管よりも多く存在する。また、前掲右上図に示すように頂点付近から管壁に沿って第二種二次流れが存在するので管壁付近の加熱された液体窒素が管中央部へ拡散され三角形管では伝熱が促進される(rh > rdp)。
正方形管でも第二種二次流れが同様に存在し、数値解析結果では平均乱流エネルギーは三角形管と円管の中間の値である [5, 6, 18]。正方形管では 4つの頂点付近に存在する液体層が三角形管よりも少なく液体層の影響が小さいので三角形管と円管の中間の特性を示す。
伝熱劣化は一般には好ましくないので、スラッシュ流体の伝熱管設計において圧力損失、熱伝達のいずれが重要かにより管断面形状を選定することになる。スラッシュ水素のみを輸送する長距離配管ではポンプ動力を低減する点から圧力損失低減が大きい円管が適しており、超伝導送電用の冷媒配管にはクエンチ伝播防止のため伝熱特性も考慮した断面形状(円管、矩形管)を選定すること、熱交換器には三角形管のように伝熱劣化の小さい断面形状を選定することが設計上有用となる。例えば、極低温機器に多用されるプレートフィン型コンパクト熱交換器を設計する上で熱伝達劣化量は重要となる。熱伝達劣化により伝熱面積が大きくなり圧力損失が増大するが、大きな圧力損失低減がこれを補うことになる。即ち、熱伝達劣化量、圧力損失低減量を定量的に把握しておくことが必要である。
円管、三角形管、正方形管の圧力損失の実験データをもとに、μSL=μL[1-(x/0.6)]-1.8で表されるみかけの粘性係数μSL、もしくは圧力損失低減が小さい三角形管、正方形管の場合には液体窒素の粘性係数μLを用いたスラッシュRe数(ReSL)と管摩擦係数λの関係式を最小自乗法により求め、流速と体積固相率xから圧力損失低減を考慮した管摩擦係数を精度良く予測できる関係式を得ている(下記 Web site)[5, 16, 20, 21]。ポンプ動力を推定する際、工学上有用となる。
* PIV法:粒子画像流速測定法 (Particle Image Velocimetry) を使用して、管内での固体粒子の流速、流跡線を直接測定した。
** 直管の圧力損失低減、伝熱劣化メカニズム:加熱時、非加熱時共に、摺動流、非均質流を経て擬均質流(均質流)となる高流速時には、管中央部に移動した固体粒子群によって管壁での乱流発達が抑制され、圧力損失低減が発生する
[16, 17]。一方、熱伝達は管壁付近の固体粒子の少ない液体層で行われるが管壁での乱流発達が抑制されるので管壁付近の加熱された液体が管中央部へ拡散する作用が抑制され、熱伝達劣化が発生する
[18, 19]。
スラッシュ窒素の流動特性、圧力損失低減と伝熱劣化特性